Logical operators

To understand the meaning of each one of the referred properties of the logical operators, the final of the article about Propositional Logic must be read.

AND

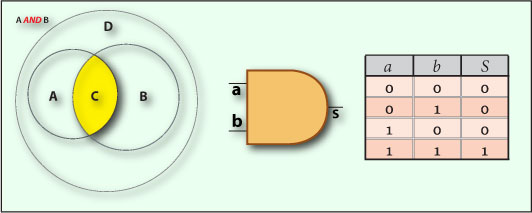
The analysis of a proposition made through a logical operator AND, or logical conjunction, results in the logical value true, if and only if all its atomic propositions have the truth value.

Let’s analyze John. He’s male, therefore he belongs to the set B, i.e. he is an object with the quality that defines the objects of the set B. He is over 20 years, so he belongs to the set A, i.e. he is an object with the quality that defines the objects of the set A.
When analyzed the proposition “John is 32 years old” or “John is male” AND “he is older than 20”, the properties a and b to be analyzed by the AND operator will be true, thus this one will be returning true too.
And Isabel, Francis and Teresa? In either case, for either of them, the properties a and/or b will assume the value 0, therefore the AND operator returning 0.

We can verify that only for the “Happy Nights” customers belonging simultaneously to the A and B sets the AND operator returns true. So, we can conclude that the AND operator defines the Intersection of the sets A and B, represented by the set C, like in the Venn diagram of Figure 1.

The algebraic expressions representing this operator could be:

a.b  or  a AND b

The Gate Symbol representing the two properties as the input operands a and b, with the values 1 or 0 and a an output S with the value 1 or 0, is shown in Figure 1.

The Truth Table for this operator, shown in Figure 1, tells us the value of its output S for the several possible combination of its input operands a and b, confirming what we’ve just verified, i.e.  the answer is true, only if both inputs are true. So we can conclude that:

The AND operator returns true for all the customers male and over 20 years, resulting a set expressed in the intersection of the sets A and B, which is C.

For the parking lot, the variable representing the presence of the car is true (1) and the variable representing the payment is also true (1), so the logic output is true (1), closing the electric circuit which opens the barrier.

OR

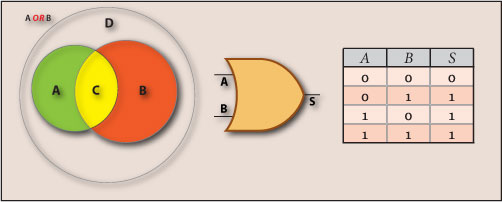
The analysis of a proposition made through the logical operator OR or logical disjunction, results in a false value, only if all  the atomic propositions are false.

Let’s analyze Elizabeth. She’s female, therefore she doesn’t belong to the set B. She’s over 20 years, so she belongs to the set A.
When analyzed the proposition “Elizabeth is 25 years old” or “Elizabeth isn’t male” OR “she’s older than 20”, the b property is false, the a property is true and the result of their analysis by the OR operator returns true.
For Francis and John, at least one of the properties a and/or b will be true and their analysis by the OR operator returns true.
Only for Teresa the properties a and b will be both false and heir analysis by the OR operator will return false.

We can verify that for any of the “Happy Nights” customers belonging to any of  the sets A or B the OR operator returns true. So, we can conclude that the OR operator defines the Union of the sets A and B, like in the Venn diagram of Figure 2.

The algebraic expressions representing this operator could be:

a+b  or  a OR b

The Gate Symbol representing the two properties as the input operands a and b, with the values 1 or 0 and a an output S with the value 1 or 0, is shown in  Figure 2.

The Truth Table for this operator, shown in Figure 2, tells us the value of its output S for the several possible combination of its input operands a and b, confirming what we’ve just verified, i.e.  the answer is false, only if both inputs are false. So we can conclude that:

The OR operator returns true for all the customers over 20 years (regardless of sex) and male (regardless of age), resulting in a set expressed by the Union of  the sets A and B.

For the parking lot case, the OR gate would be the correct gate to verify either the electronic toll payment or the paid card introduction, returning true when any of them would be true. Being its output connected to the AND gate input referring to the payment, once the payment is made by either way and the car is in position, the AND gate logic output is true (1), closing the electric circuit which opens the barrier.

NOT

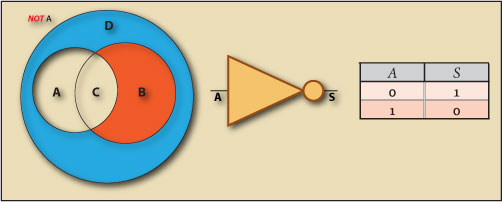
The analysis of a proposition with the logical operator NOT or logical inverter, results true if the atomic proposition is false and vice versa.

Let’s analyze Francis.  He’s younger than 20, thus not belonging to the A set .
When analyzed the proposition “Francis is 18 years old” or “Francis” NOT “is older than 20”,  the a property is false and the result for its analysis returned by the NOT operator is true.
For Teresa the NOT operator also returns true, but for John and Elizabeth it returns false, as both they are older than 20.

We can verify that for any of the “Happy Nights” customers who doesn’t belong to  the A set  the NOT operator returns true. So, we can conclude that the NOT operator defines the Difference of the A set, like in the sets Venn diagram in Figure 3.
This is the case represented in this Figure but the same goes for the set B.

The algebraic expressions that represent this operator could be:

¬a  or  NOT a

This operator Gate Symbol and Truth Table are represented in Figure 3. We can conclude that:

The NOT operator represents all the customers under 20 years regardless their gender, when analyzed their age, resulting in a set expressed by the Difference of A, or all the female customers regardless their age, when analyzed their sex, resulting in a set expressed by the Difference of B.

For the parking lot, the NOT gate should be the appropriate one to put after the AND gate in a diverting circuit to close the barrier. Thus, when the car leaves, the AND gate returns a false value (0), resulting in a true output for the NOT gate, thus opening the circuit that closes the barrier.

That completes the presentation of the basic Boolean operators. Basic because the others are achieved through the combination of these.
We have four more operators to consider, which are NAND, NOR, XOR and XNOR.

NAND

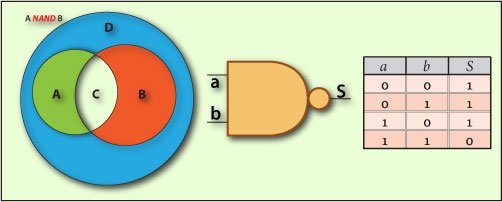
NAND, or denial of the logical conjunction, usually expressed as “NOT (this AND that)” is a logical operator obtained through the operators AND and NOT using the relation NOT(A AND B) = A NAND B .

A proposition analyzed with a NAND operator, produces a false value only if both its atomic propositions are true, i.e. NAND produces a true value if at least one of its atomic propositions is false.

Regarding Elizabeth, Teresa and Francis at least one of the variables a and/or b, assumes the value false, since either of them is false over at least one of its properties, Teresa and Elizabeth for the age and Francis for the gender. The analysis made with the NAND operator to anyone of them will return true.
Regarding John, both variables a and b assume the value true. The analysis by the NAND operator returns the value false.

We can verify that for any of the “Happy Nights” customers not belonging simultaneously to both  the sets A and B, i.e. who doesn’t belong to their Intersection, the NAND operator returns true.
So, we can conclude that the NAND operator defines the Difference of the Intersection of A and B, as it defines the set with the objects who don’t belong to their Intersection, like in the Venn diagram in Figure 1.

The algebraic expressions representing this operator could be:

¬(a . b)  or  a NAND b or NOT (a AND b)

The Gate Symbol and Truth Table for this operator are represented in Figure 1. We can conclude that:

 The NAND operator returns true for all the customers but those who are male over 20, resulting a set express by the Difference of A and B intersection.

In ours parking lot case, if we could imagine that we wanted that while isn’t simultaneously verified that the car at the entrance has already received the ticket to get in and his no longer present (being given by NOT operator the indication to close the barrier), a new ticket won’t be provided to the next car.
By other means, if the car has received a ticket (1) and it’s at the entrance (1), NAND returns the value false (0) and doesn’t trigger the mechanism to issue a new ticket, because the circuit will be kept  opened. This analysis is supposed to happen after the actions described before.

NOR

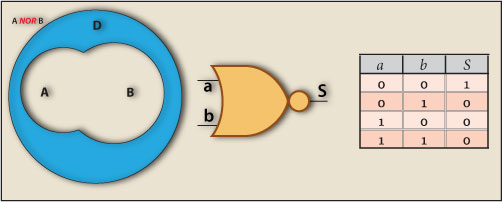
NOR or denial of logical disjunction, usually expressed as “NOT (this OR that)”,  is obtained through the combination of the logical operators NOT and OR using the relation NOT (A OR B) =  A NOR B.
A proposition analyzed with a NOR operator,  produces a false value if at least one of its atomic propositions is true, i.e. the NOR operator produces a true value only when both its atomic propositions are false.
Regarding John, Elizabeth and Francis, at least one of the variables a and/or b assumes the value true, since either of them is true over at least one of its properties, John and Elizabeth for the age and Francis for the gender. The analysis made with the NOR operator to anyone of them will return false.
Only for Teresa both variables a and b are false, thereby resulting from the application of the NOR operator a true value.

We can verify that for any of the “Happy Nights” customers not belonging to any of  the sets A or B, i.e. who doesn’t belong to their Union, the NOR operator returns true.
So, we can conclude that the NOR operator defines the Difference of the Union of A and B, as it defines the set with the objects who don’t belong to their Union, like in the Venn diagram in Figure 2.

The algebraic expressions representing this operator could be:

¬(a+b)  or  a NOR b or NOT (a OR b)

The Gate Symbol and Truth Table for this operator are represented in Figure 2. We can conclude that:

The NOR operator returns true for the female customers under 20 years, resulting a set express by the Difference of the Union of A and B.

The parking lot we have been analyzing has two difficult limitations: It can’t let in cars over 1.80 meters in height, due to availability of effective floors height, or over 4.20 meters in length, due to the radius of the ramp curve.
For this reason there have been installed sensors that determine the height and length of the cars at the park entrance, producing 1 or 0 values as its true or false that they are above those measures and connected them to a NOR gate inputs.
Only if both sensors return 0 an output 1 will tell the AND gate, through a proper circuit, that the barrier can be opened.
It’s not our purpose to create the circuit for this effect, but just to satisfy the curiosity, the NOR output can be connected to a 1st AND gate input where the car presence detector is connected too. Then, this 1st AND gate output can be connected to the AND gate which verifies the car presence and the payment. So being, only when NOR returns 1 the barrier can open.

Notice how, even being only describing the most basic expressions of propositional logic, we have the access of a car parking controlled with a series of checks. And we do it only by analyzing true or false, 1 or 0 with logic gates, now integrated in small circuits.

XOR

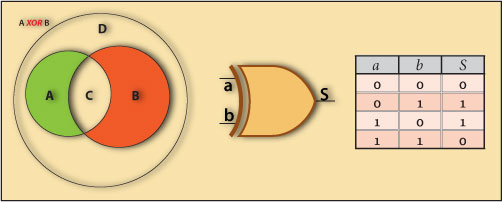
XOR  or eXclusive OR, its a logical operator also known as the Difference operator or yet exclusive disjunction.
A proposition analyzed by the XOR operator returns true when, being true one of its atomic propositions the other is false and vice versa. Exclusive Or means precisely always one of them but never both of them. Difference Operator means always different, never coincident.

Let’s analyze Elizabeth. She’s female, therefore she doesn’t belong to the B set . She’s over 20 years, so she belongs to the A set .
When analyzed the proposition “Elizabeth is 25 years old” or “Elizabeth isn’t male” XOR “she’s older than 20”, the b property is false, the a property is true and the result of their analysis by the XOR operator returns true, as both properties have different values for her.
For Francis, the b property is true and the a property is false, thus its  analysis by the XOR operator returns true.
For John and Teresa the a and b properties will be both true or false respectively and their analysis by the XOR operator will return false.

We can verify that for any of the “Happy Nights” customers belonging to any of  the A or B sets but never belonging to both of them, the XOR operator returns true, i.e. XOR returns true for the objects inside the Union of both sets but outside their Intersection.
So, we can conclude that the XOR operator defines the Symmetric Difference of the A and B sets, like in the Venn diagram of Figure 1.
The algebraic expressions to represent this operator can be:

a ⊕ b  or  a XOR b

This operator Gate Symbol and Truth Table are represented in Figure 1. We can conclude that:

The logical operator XOR returns true for the females over 20 years and males under 20 years, resulting in a set expressed by the Symmetric Difference of sets A and B.

This time we are going to leave the parking lot and hold us in the “Happy Nights” to demonstrate an automation action through a XOR gate.
The “Happy Nights” owner decided to control the access of all customers using an automated manner. Therefore he created a customer card that granted access to the club. Who wanted to get access needed to be cardholder or ask to create one before joining.
Only after the card was inserted in a card reader at the club’s entrance, once transferred the data into the computer (I-Input) and processed, the computer issued a comand to the entrance barrier (O-Output) allowing or not the customer to get in, according to the instructions it was given.
Let’s assume that, for unknown reasons belonging only to the imaginary, the owner ordered that only women over 20 years and men under 20 years could get into “Happy Nights” that day.
In order to do so, the card reader was connected to a XOR gate to witch inputs it sent the values of the a and b properties read from each customer’s card. The XOR gate output, when 1 closed the electric circuit which opened the entrance barrier.
This way, when the customer was a male (b=1) it had to be younger than 20 (a=0) and when it was a female (b=0) it had to be older than 20 (a=1), for the XOR gate to allow them to get in.
Accordingly, that day only Elizabeth and Francis could get into the club. John and Teresa stayed at the door.

XNOR

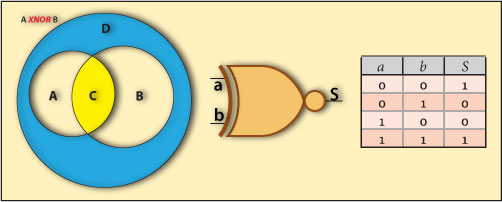
 XNOR is a logical operator also known as a Coincidence operator whose operation is the inverse of XOR, i.e.  a XNOR b = NOT (a XOR b).
A proposition analyzed through a XNOR operator returns true when both their atomic propositions are true or false. Coincidence operator means always coincident, never different.

Elizabeth and Francis, for whom the properties a and b are different, when analyzed by a XNOR operator returns false.
John and Teresa, for whom the properties a and b are coincident, when analyzed by a XNOR operator returns  true.

We can verify that for any of the “Happy Nights” customers simultaneously belonging to both  the sets A or B or to none of them, the XNOR operator returns true.  XNOR returns true for the objects inside the Intersection of both sets or outside their Union, where the properties a and b for them  are always coincident, i.e. both true or both false.
So, we can conclude that the XNOR operator defines the Symmetric Identity of the sets A and B, like in the Venn diagram ofFigure 2.

The algebraic expressions representing this operator could be:

a ≡ b  or  a XNOR b

This operator Gate Symbol and Truth Table are represented in Figure  2. We can conclude that:

The logical operator XNOR returns true for the female clients under 20 and for the male clients over 20, resulting in a set expressed by the Symmetric Identity of A and B.

We’ll still hold us in the “Happy Nights” to demonstrate an automation action through a XNOR gate. Now the owner wants exactly the opposite, i.e. tonight only females under 20 and males over 20 can get in.
In order to do so, the card reader is now connected to a XNOR gate to witch inputs it sends the values of the a and b properties read from each customer’s card. The XNOR gate output, when 1 closes the electric circuit which opens the entrance barrier.
This way, when the customer was a male (b=1) it had to be older than 20 (a=1) and when it was a female (b=0) it had to be younger than 20 (a=0), for the XNOR gate to allow them to get in.
Accordingly, that day only John and Teresa could get into the club. Elizabeth and Francis stayed at the door.

Tristate gates

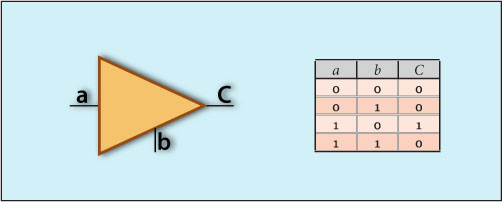
Tristate gates as we can see in Figure 3 admit three output states:

• 0 or 1 as the of the input a value is 0 or 1 when the input b is Enabled or
• Off if the input b isn’t Enabled.

A Tristate gate can be Enabled either by a 1 or 0 value of b. We will analyze the Tristate gate active or enabled at 0, thus by b=0.
A Tristate gate is basically a switch that either lets through its input (b=0) or simply is turned off not letting through any input (b=1).
Tristate gates are typically used when multiple lines are attempting to share a single line where only one signal at a time can be present, under  the penalty of causing short circuitries.
By having a Tristate gate in each of the lines which connects with the single line, we ensure that only one of their signals is present at a time. It’s critical to ensure that only one Tristate gate is active at a time, otherwise the circuit can be destroyed.
Later on we’ll see some cases of these gates’s application

Multiple Entries Logic Gates

So far we have spoken of  logical operators and presented  the symbols by which they will be named from now on,  the logical gates, which are the physical symbol for the operators abstraction.
Its in this quality that the logical operators are going to integrate the logical circuits as we’ll see further on.
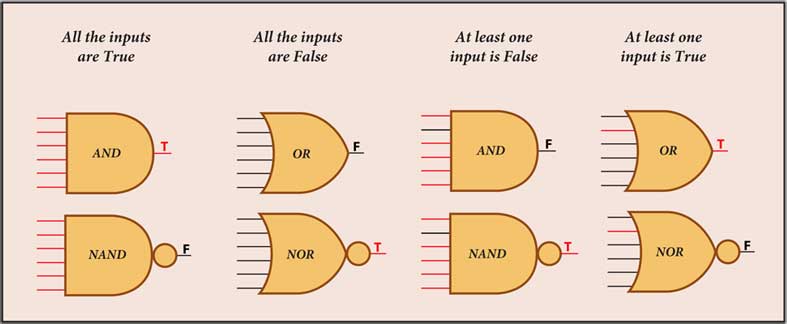
We’ve analyzed the logical gates always with two inputs, but actually they can have several inputs, and the reference should be done like this.

• The output of an AND gate is true only if all the inputs are true and false is at least one input is false.
• The output of an OR gate is false only if all inputs are false and will be true if at least one input is true;
• The output of a NAND gate is false only if all inputs are true and will be true if at least one input is false;
• The output of a NOR gate is true only if all inputs are false and will be false if at least one input is true;

as can be seen in  Figure 3.

Conclusion

We have seen how, with the logical operators, we can influence decisions based on assumptions. The Logical operators are in the understanding of human reasoning, created by us to work the duality true / false. With the combination of these operators, or rather gates, we can built circuits that allow us to perform what we call programs, in its most elementary form.
The logic gates are abstractions created in the human mind that allow us to create more complex abstractions, supported in logical reasoning.
But the computer doesn’t understand abstractions. The computer has no reasoning. The computer is an excellent performer of what we instruct it to do. In fact the computer knows only two states in order to understand their circuits: with or without voltage.
It was man as a thinking being, that took what Mr. George Boole did with binary mathematics and philosophical logic and said that those states of the computers electrical circuits went on to represent the logic states 1 and 0 of Boolean algebra. It was the association between electrical circuits and Boolean algebra that made possible the wonderful machines without whom we would almost return to the stone age.
But, apart history, in fact we don’t yet know how the abstraction built in the human mind with true or false states is converted into voltage states in the computer’s circuits. Resuming, how abstraction became physical.

And that’s the real secret of the birth and evolution of the computer. Thus, let’s see how abstractions are materialized in electric circuits.  But in the next Chapter.