Set Theory

We’ll try to start with the set theory in order to better understand the logic that we used to introduce the logic operators.

Set

A Set represents a group of objects which satisfy a given property that characterizes it. Having that property those objects belong to its domain.
A set by itself doesn’t have a definition that clearly says what it is. We need to associate it with the term object and with the belonging quality, in order to understand what it is. A set Domain refers to all the objects that belong to it.
Let’s go back to George’s nightclub, the “Happy Nights”. Now let’s look to the set of “Happy Nights” customers. The property that defines this set is being its customers. The objects of the set are all the persons from the people universe that have the common property of being “Happy Nights” customers, thus belonging to that set.

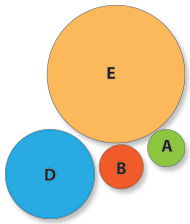
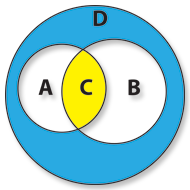
A set can have any shape. It isn’t but an abstract concept  of group where we include the objects with a same property that gives them the quality of belonging to it. Typically they are represented by the Venn diagram, where each circle defines the area of a given set, characterized by a property of the objects belonging to it:

• E, representing the set of all the “Happy Nights” customers, i.e. the set of persons from the people’s universe who have in common the e property of being “Happy Nights” customers.
• D, representing the set of  “Happy Nights”  customers who have the common d property of being present there.
• A, representing the set of “Happy Nights” customers there present who have in common the a property of being over 20 years old.
• B, representing the set of “Happy Nights” customers there present who have in common the b property  of being male.

As we can see the objects of the different sets represented have common properties, i.e. there are persons who, by their characteristics, belong to several sets. So, let’s put the sets in their right place.

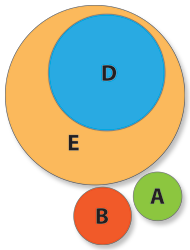
The D set represents the “Happy Nights” customers (property e) who are present there (property d), i.e. they belong to the D set and to the E set too. Let’s put the D set in its right place.
Why didn’t we put the D set taking all the E set space?
Because there are certainly many “Happy Nights” customers that are not present there, not having the d property and thus not belonging to the D set.
We say that the E set contains the D set or that the D set is contained by the E set.

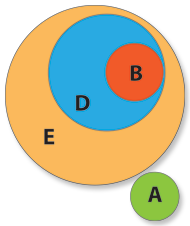
The persons belonging to the B set have the common  b property of being male, but they have too the common properties of being “Happy Nights” customers (the e property) and being there (the d property). So, 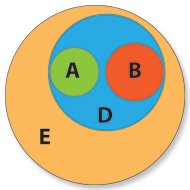let’s put the B set in its correct place. The B set is contained by the D set.

The same goes for the persons who belong to the A set, having the a common property of being older than 20 years, thus putting the A set into its correct position. A is contained by D.

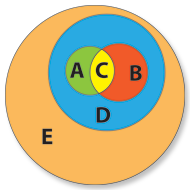But there will certainly be inside the “Happy Nights” some customers older than 20 years and male, i.e. there will be persons that being “Happy Nights” customers (property e) and being there (property d) are male (property b) and older than 20 (property a). So, let’s put the sets A and B in the appropriate positions.

Once understood the content of the sets we are going to work with and having all them set in the appropriate positions, it’s now time to analyze how to define the relation between the several objects within the set D according to their properties.
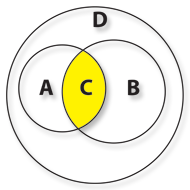Let’s now forget about the E set and get worried only with the customers which are inside the “Happy Nights”, the D set. With those we are going to build the possible combinations with their properties and find names for them. For now we know that D contains A and B.

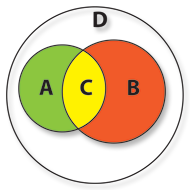If we want to represent the customers inside “Happy Nights” that are older than 20 and male, we’ll have to use the C set, which is the Intersection of the sets A and B,  corresponding to the customers of the domains of both sets A and B which simultaneously have both the properties a and b.

If we want to represent the customers inside “Happy Nights” who are male (regardless of age) and are over 20 (regardless of gender), then we’ll have to use the Union of the sets A and B, corresponding to all the clients of A and B domains, 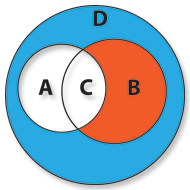including those belonging simultaneously to both.

If we want to represent all customers inside “Happy Nights” who are younger than 20 , we’ll have to use the whole domain of D excluding the domain of A, i.e. the Difference of A.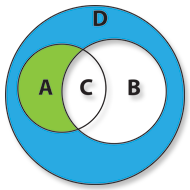

If we want to represent all the female customers inside “Happy Nights”, we’ll have to use the whole domain of D excluding the domain of B, i.e. the Difference of B.

If we want to represent all customers inside the “Happy Nights” who are not males over 20, we have to use the Difference of the intersection of A and B.

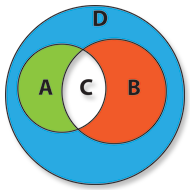If we want to represent all customers inside the “Happy Nights” who are female under 20, we have to represent the Difference of the union of A and B.

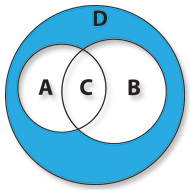If we want to represent all customers inside the “Happy Nights” who are female over 20 and male under 20, we have to use the objects of D representing the Symmetric difference regarding the sets A and B. This set corresponds to the objects of  both sets union , excluding their intersection.
Actually, when any customer in this group returns true to the property that gives him the quality to belong to one of the sets it will return false to the property that gives him the quality to belong to the other set. Hence its name. The customer will be a she greater than 20 (a is true and b is false) or a he less than 20 (a is false and b is true).

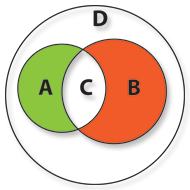If instead we want to represent all customers inside the “Happy Nights” who are male over 20 and female under 20, we’ll use the set of objects of D that corresponds to the Symmetric identity (the Difference of the Symmetric difference) regarding the sets A and B. This set corresponds to the difference of the union of both sets added with their intersection.
Actually, when any customer in this group returns true to the property that gives him the quality to belong to one of the sets it will return also true to the property that gives him the quality to belong to the other set. Hence its name. The customer will be a she younger than 20 (a and b are both false) or a he greater than 20 (a and b are both true).

Everything we’ve seen so far about Set Theory will be applied to the analysis of logical operators.

Propositional Logic

“The customer of the club is over 20 years” or “The disco customer is male” are examples of statements that any of us can produce and that can take the state of true or false, according to the name of the person we put as club customer, its age and gender properties.
In propositional logic, a statement that can assume the state of true or false, is called a proposition.
But in this case, none of the statements that we produced is decomposable into others. In propositional logic, a statement that is not decomposable and can take the state of true or false, is called an atomic proposition.
Now let’s say: “The customer of the nightclub is over 20” AND “it is male”. Now we have a statement that is decomposable into two atomic statements. These two atomic statements are now joined by the word AND (a logical operator that we will soon see what it means), converting two atomic propositions into a statement. However, it is still a statement that can take the state true or false, therefore being a proposition.
The statements included in a proposition, may even involve formulas expressing relationships between other statements established with logical operators, but the  final answer will always be only one of two possible: true or false.
Thus, the propositions represent the formulas of propositional logic or propositional calculus. We can now define propositional logic or propositional calculus:

Propositional Calculus is a system in which formulas representing propositions can be built by combining atomic propositions using logical operators.

To realize why the themes of propositional logic and set theory were introduced here, we have to go back in time and make a little history.

Boolean Algebra

In 1854, the British mathematician George Boole, through the work entitled “An Investigation of the Laws of Thought”, presented a mathematical system of logical analysis known as Boolean algebra, mathematical theory based on algebraic structures that capture the essence of the logical operations AND, OR and NOT, as well as from set theory. The Boolean algebra was an attempt to use techniques for dealing with algebraic expressions in propositional calculus
We hope that at this stage of your knowledge evolution, you’ve already realize the importance of what Mr George Boole did. The Boolean algebra was developed based on older concepts of Greek philosophers about logic. So, George Boole created algebraic structures that worked the duality true/false in statements through logical operators. He created what would become the propositional calculus or propositional logic.
George Boole, without knowing it and with nearly a century in advance, built the foundation of computational mathematics, based on binary numbers.
Boolean algebras were applied for the first time to switches by Claude Shannon in the twentieth century, who demonstrated that the application to electric circuits of Boolean algebra could solve any logical and numerical relation.
A Boolean variable can assume only two values: 1 and 0, or true and false, as for instance:

• One light bulb on (1) or off (0)
• One door closed (1) or opened (0)
• One switch closed (1) or opened (0)

And its representation can be made by:

• Symbols (Logic Gates) which are  the application of the logical operator’s concept to a physical representation of something that can be included in a logic circuit.
• Logical algebraic expressions.
• Truth tables, consisting of tables with the output value for all possible combinations of the input values.

Logical operators

We mentioned logical operators for several times and have not yet define them. But its definition has to be done with time and space, to be understood. You’ve certainly already realize that the secrecy of computer capabilities comes through them.

In order to define the Logical Operators we’ll analyze a group of objects using the concepts of propositional logic and building the propositions which will return true or false according to the object and the property in analysis. This way we’ll define the set where to each object belongs  and each set content after the analysis of all the group of objects.
The properties which are going to be used to analyze the objects are:
a – being over 20 years.
b – being male.
The objects that are going to be analyzed under these properties are the “Happy Nights” customers, thus becoming members of the sets A or B, as the propositions defining each customer qualities regarding the properties a and b return true.
For instance, the proposition “George is 18 years old” is decomposable in two atomic propositions which return true for the property b (“George” – he is male) and false for the property a (“is 18 years old” – he is younger then 20), reason why he has the quality which grants him to belong to the B set, but not to the A set.
We wanted to make clear the difference between the properties a and b, which define each customer specific qualities, being part of the propositions to analyze and the sets A and B, each being composed by the group of objects (customers) for which the propositions will return true.
As a way to become more objective in the analysis we will focus in the concrete situation of  the following 4 customers of the “Happy Nights”:

• John (b), 32 years old (a):
  a is true, so a=1.
  b is true, so b=1.

• A Isabel (b), 25 years old (a):
  a is true, so a=1.
  b is false, so b=0.

• O Francisco (b), 18 years old (a):
  a is false, so a=0.
  b is true, so b=1.

• A Tereza (b), 18 years old (a):
  a is false, so a=0.
  b is false, so b=0.

We will also try to imagine one situation of production automation, without human intervention and depending on the information that certain devices provide to the computer, which makes a decision that triggers other devices. We will use the same example we have dealt with at the beginning: the car parking lot.

Let´s proceed to the analysis of the logical operators.

But in the next article.