The Sound

Sound comes from different air compressions, resulting from different vibrations such as: the vibration of the vocal cords (voice), the vibrating strings of a violin, the vibrating strings of a piano, the vibration of a drum, the vibration of the reed of a horn, the vibration of a speaker, etc.

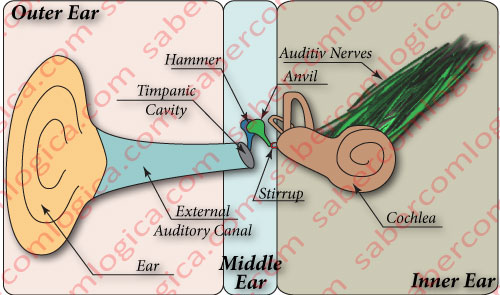
There must be a source producing the sound. And that sound is audible for us humans due to the constitution of our ear, which is represented in Figure 1:

• The outer ear constituted by the ear and the external auditory canal, whose function is to capture and transmit the air pressure variations through the channel.
• The middle ear, whose function is to convert those pressure variations into vibrations, through the use of the eardrum (tympanic membrane), which is connected to a set of three small bones, the hammer (malleus), the anvil (incus) and the stirrup (stapes). This set of 3 little bones captures and magnifies the effect of the vibrations of the eardrum and transmits them to the inner ear.
• The inner ear constituted by a snail-shaped, liquid filled, bone structure, the cochlea, to which the stirrup transmits the magnified vibrations. This cavity is, in turn, enveloped by thousands of nerve terminals, each transmitting specific frequency information to the brain.

It is in the brain that this information is transformed into the sound we can hear, and can be either irritating noise, or a harmonic music.

These changes in the air pressure are picked up by microphones, which convert them to electromagnetic waves, as shown in Figure 2. Devices like the microphone, which converts between different forms of energy, in this case acoustic to electromagnetic, are called transducers.

Until now, we only spoke about analog values. It’s now time to convert from analog to digital, starting with our new electromagnetic wave.

Analog to Digital

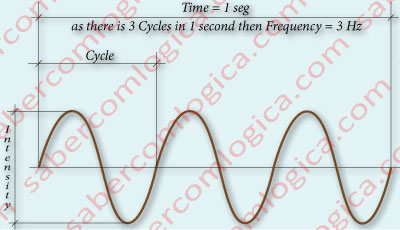
In a simple and uniform representation of a sound wave, we have emphasized its main characteristics, intensity and frequency, as shown in Figure 3.

• The intensity is the value of the difference between the highest and the lowest wave peaks.
• The frequency is the number of cycles repeated by second. It is measured in Hz, or cycles/second.
• The cycle is the difference between two points where the shape of the wave repeats itself.

 A sound wave is a lot more complex than the waves we have been showing, but keep in mind that this work is not actually about sound, but rather about how sound is digitalized.

Continuing with our simple wave, let’s now represent its digitalization at 4 bits (0 to 15) with a reduced sampling, as shown in Figure 4. The digital waveform that results from the collected sampling is represented in blue.

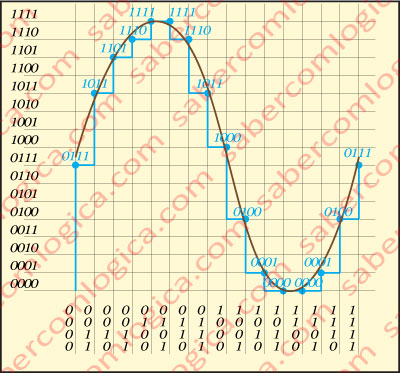
The grid of lines and columns represents binary values ​​of 4 bits, from 0000 (0) to 1111 (15), evolving from the origin of both the X and Y-axis.

The blue line (digital wave) represents, at each point, the closest binary value of the Y-axis, at each intersection of the analog wave with the sequential binary values from X-axis. The resulting binary values at each point are represented near that point in blue.

The binary representation of this simple piece of sound wave, with this reduced sampling, and so few bits, would be:

0111 1011 1101 1110 1111 1111 1110 1011 1000 0100 0001 0000 0000 0001 0100 0111

But, both the number of bits used to represent the different values ​​of the wave, as well as the sampling rate, are very different from reality, if we consider the complexity of a sound wave, and the need to represent it in a reliable fashion.

If we listened to music recorded in these conditions, we would only hear a succession of sounds (portions of what we wanted to record), which would only seem vaguely similar to what was being recorded with a great dose of imagination and good will.

The conversion is performed by devices known as ADC (Analog Digital Converter), for whom the sampling frequencies and the bit representation are defined in each case. An ADC that converts audio CD (a file type WAV, short for WAVE – Waveform Audio File Format) uses a sampling frequency of 44,100 Hz, meaning it collects 44,100 samples per second, and each sample is represented by 16 bits, equating to 65,536 different values. These values are for a single stereo channel, and given that there are 2 stereo channels, we need to double them.

Therefore, a 3 minute stereo music, recorded in audio CD (WAV), would have the size of

[44.100 samples/s] x [16 bits x (3 x 60)s] x [2 channels] = 254.016.000 bits = 31.732.000 Bytes  ≈ 30 MB

which effectively corresponds to the size of an actual audio CD music, as we can easily verify.

It’s the same as if we were to insert 44.100 columns and 65.536 lines in Figure 4, instead of the 16 columns and 16 lines.

Well, now we have our music recorded on a CD in WAV format, in the form of numbers. Many ones and zeroes one after the other.

WAV is a non-compressed format. As an example of a compressed format we will mention the MP3 (MPEG Audio Layer 3). With a bit rate of 128 Kb/s, it reduces the file size to about 10% of the original, while keeping a reasonable sound quality. Bigger or smaller bit rates will result in a better or worst final sound quality.

MP3 is the standard format for audio compression (standard must be read as the most used and accepted format in the commercial market) for file transfers and audio reproduction in digital audio reproducers.

Let’s get back to the digital WAV file, which we recorded digitally, or rather, in numbers. But we can’t hear numbers. We can only hear sounds, the changes in air pressure. So, how can we listen to it?

Digital to Analog

To listen to the recorded music, we have to convert the recorded numbers into different air compressions, audible to our ears. To do this, we will use a device with the name of DAC (Digital Analog Converter) which will convert the numbers into electromagnetic waves, and we will again use a transducer, that will convert the electromagnetic waves into vibrations that will produce different air compressions.

The DAC, by an inverse process of the ADC, converts the digital signals into electromagnetic waves.

Since the conversion is made from a squared wave, the digital one, to obtain a good sound quality, some interpolation must be done to the spaces left between the samples (like in the green points of Figure 5), in order to give to the wave a smoother shape, more similar to the original.

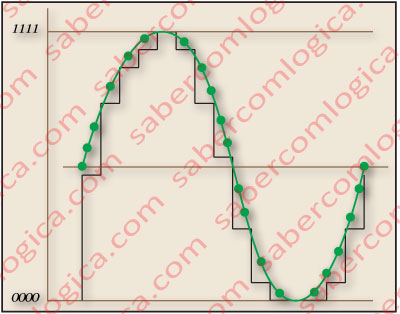
This process is called oversampling, and its accuracy is directly proportional to the complexion and cost of the DAC. Let’s simplify, and refer to the DAC by the name of our old friend, the CD player.

The common CD players have now reached bargain prices, but a good high fidelity CD player, used to reproduce sound for high-accuracy systems, intended for very demanding audiophiles, are not yet very affordable.

Beyond a rigorous selection of high quality components, the main difference lies in high oversampling rates, through very complex proprietary algorithms, which make the sound read from the digital source incredibly similar to the analog original.

The problem is that this difference costs money, lots of money, and it’s the fundamental

reason why some people say they don’t like digital sound. When they buy a CD player, they tend to choose the less expensive one. In reality, the numbers on the CD are equal for everyone, and read the same way. We hope you understood where the difference lies. Let’s go on.

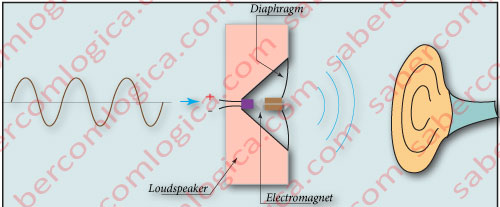
Once obtained the original wave, it is then redirected to a loudspeaker, where the activation of the core’s electromagnet, due to electrical impulses, makes the diaphragm vibrate, which in turn causes variations in air pressure, thus creating the sound we hear, as we can see in Figure 6.

And there we have it. We’ve gone back to the starting point.