Teoria dos Conjuntos

Vamos tentar partir da teoria dos conjuntos para mais facilmente entendermos a lógica que vamos usar para introduzir os operadores lógicos.

Conjunto

Um Conjunto corresponde a um grupo de objetos que cumprem uma determinada propriedade que  o caracteriza e que, por terem essa propriedade, pertencem ao seu domínio.
Um conjunto só por si não tem uma definição que diga claramente o que é. Precisamos de lhe associar o termo objeto e a qualidade pertença para que se entenda o que é. O Domínio de um conjunto refere os objetos que lhe pertencem.
Vamos voltar à discoteca onde o Tozé era porteiro. A discoteca “Noites Felizes”. E vamos olhar para o seu  conjunto de clientes.
A propriedade que define o conjunto é serem clientes da discoteca “Noites Felizes”. Os objetos do conjunto são os indivíduos do universo das pessoas que são clientes da discoteca “Noites Felizes” e que por essa razão pertencem ao conjunto.
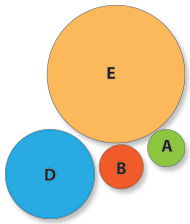Um conjunto pode ter qualquer forma. Ele é simplesmente um conceito abstrato de agrupamento de objetos com a mesma qualidade que os define como lhe pertencendo. Normalmente representam-se pelo diagrama de Venn, em que cada circulo define o domínio de um determinado conjunto caracterizado por uma propriedade dos objetos que lhe pertencem:

• E representa o conjunto de todos os clientes da “Noites Felizes”, i.e. o conjunto do universo de indivíduos que têm em comum a propriedade e de serem seus clientes.
• D representa o conjunto dos clientes da “Noites Felizes” que têm em comum a propriedade d de lá estarem presentes.
• A representa o conjunto dos clientes presentes na “Noites Felizes” que têm em comum a propriedade a de terem mais de 20 anos.
• B representa o conjunto dos clientes presentes na “Noites Felizes” que têm em comum a propriedade b de serem do sexo masculino.

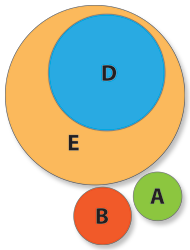Como se pode verificar os elementos dos diversos conjuntos representados têm propriedades em comum, i.e. há indivíduos que pelas suas características pertencem a vários conjuntos. Vamos então coloca-los nas devidas posições.

O conjunto D representa os clientes da “Noites Felizes” (propriedade e) que presentemente lá se encontram (propriedade d), i.e. eles pertencem ao conjunto D mas também ao conjunto E. Vamos então colocar o conjunto D no devido lugar.
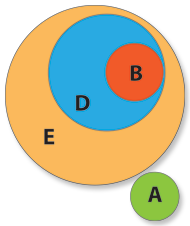E porque não colocámos o conjunto D a ocupar todo o espaço do conjunto E?
Porque certamente há muitos clientes da “Noites Felizes” que neste momento não estão presentes, não tendo a propriedade d e portanto não pertencendo ao conjunto D. Diz-se neste casso que o conjunto E contém o conjunto D ou que o conjunto D é contido pelo conjunto E.

Os indivíduos que pertencem ao conjunto B têm em comum a propriedade b de serem do sexo masculino, que lhes confere essa qualidade de pertença. Mas eles também são clientes da “Noites Felizes” (propriedade e) e estão presentes 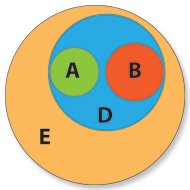propriedade d). Vamos então colocar o conjunto B no local correto. Da mesma forma o conjunto B é contido pelo conjunto D.

O mesmo se passa com os indivíduos que pertencem ao conjunto A, com a propriedade a de serem maiores de 20 anos. 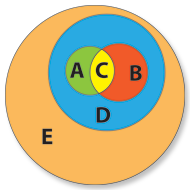Vamos então colocar o conjunto A no local correto. O conjunto A é contido pelo conjunto D.

Mas haverá certamente entre os clientes presentes na “Noites Felizes” alguns que tendo mais de 20 anos são também do sexo masculino, i.e.  haverá pessoas que sendo clientes da “Noites Felizes” (propriedade e) e estando lá presentes (propriedade d) são do sexo masculino (propriedade b) e têm mais de 20 anos (propriedade a). Vamos então colocar os conjuntos A e B nas posições correspondentes a esta situação.
Percebido o conteúdo dos conjuntos com que vamos trabalhar e colocados todos na  posição apropriada, chega agora a ocasião de entendermos como se define o relacionamento dos vários objetos do conjunto D conforme as suas propriedades.
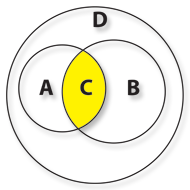Vamos esquecer o conjunto E e preocupar-nos só com os clientes que se encontram presentes na “Noites Felizes”, o conjunto D. Com esses vamos formar os diferentes tipos de combinações possíveis e encontrar para elas nomes. Para já sabemos que D contém A e B.

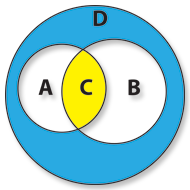
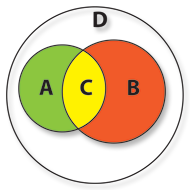Se quisermos representar os clientes da “Noites Felizes” que em simultâneo têm mais de 20 anos e são do sexo masculino, vamos ter que usar o conjunto C, que é a Intersecção dos conjuntos A e B, correspondente aos clientes do domínio de ambos os conjuntos que detêm em simultâneo as propriedades a e b.

Se quisermos representar os clientes do sexo masculino (independentemente da idade) com mais de 20 anos (independentemente do sexo), então vamos ter que representar a União dos conjuntos A e B, correspondente a todos os clientes do domínio de ambos os conjunto, incluindo os que pertencem em simultâneo aos dois.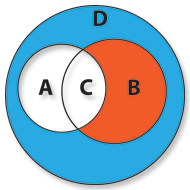

Se quisermos representar os clientes menores de20 anos presentes na discoteca teremos que representar todo o domínio de D com exclusão do domínio de A, ou seja a Diferença de A.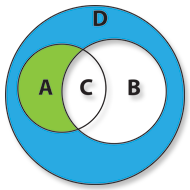

Se quisermos representar os clientes do sexo feminino presentes na discoteca teremos que representar todo o domínio de D com exclusão do domínio de B, ou seja a Diferença de B.

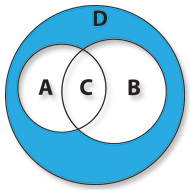
Se quisermos representar todos os clientes na discoteca com exceção dos que são do sexo masculino com mais de 20 anos, teremos que representar a Diferença da Intersecção de A com B.

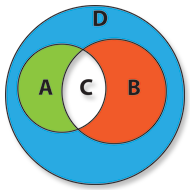Se quisermos representar todos os clientes do sexo feminino com menos de 20 anos, teremos que representar a Diferença da União de A com B.

Se quisermos representar os clientes do sexo feminino maiores de 20 anos e do sexo masculino menores de 20 anos, teremos que representar o conjunto dos objetos de D que representam a Diferença Simétrica relativamente aos conjuntos A e B. São os objetos que pertencem à união dos dois conjuntos com a exclusão da sua intersecção.
Na realidade, quando qualquer cliente deste grupo devolver verdade para a propriedade que lhe dá a qualidade de pertencer a um dos dois conjuntos devolve falso para a propriedade que lhe daria a qualidade de pertencer ao outro. Daí o nome. Ou é uma ela maior de 20 anos (a é verdadeira e b é falsa) ou um ele menor de 20 anos (a é falsa e b é verdadeira).

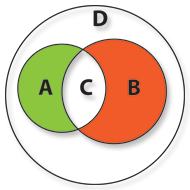Se pelo contrário quisermos representar os clientes do sexo masculino maiores de 20 anos e do sexo feminino menores de 20 anos, teremos que usar os objetos de D que representam a Identidade Simétrica relativamente aos conjuntos A e B. São os clientes que pertencem à Diferença da União desses dois conjuntos, acrescidos dos clientes que pertencem à sua Intersecção.
Na realidade, quando qualquer cliente deste grupo devolver verdade para a propriedade que lhe dá a qualidade de pertencer a um dos dois conjuntos devolve também verdade para a propriedade que lhe daria a qualidade de pertencer ao outro. Daí o nome. Ou é uma ela menor de 20 anos (a e b são ambas falsas) ou é um ele maior de 20 anos (a e b são ambas verdadeiras).

Tudo o que até agora vimos sobre conjuntos se vai aplicar à análise dos operadores lógicos.

Lógica Proposicional

“O cliente da discoteca tem mais de 20 anos” ou “O cliente da discoteca é do sexo masculino”,  são exemplos de afirmações que qualquer um de nós pode produzir e que podem assumir o estado de verdadeiras ou falsas, conforme o nome da pessoa que colocarmos no lugar de cliente da discoteca e as suas propriedades de idade e sexo.
Em lógica proposicional, a uma afirmação que pode assumir o estado de verdadeira ou falsa, chama-se proposição.
Mas, neste caso, qualquer uma das afirmações que produzimos não é decomponível em outras. Vale por si só.
Em lógica proposicional, a uma afirmação não decomponível que possa assumir o estado de verdadeira ou falsa, chama-se proposição atómica.
Mas se dissermos “O cliente da discoteca tem mais de 20 anos” E “O cliente da discoteca é do sexo masculino” passamos a ter uma afirmação que é decomponível em duas, as que vimos primeiro, que estão unidas pela palavra E, ou seja, por um operador lógico, E ou AND (já vamos perceber o que são operadores lógicos, em local próprio).
No entanto, continua a ser uma afirmação que pode assumir o estado de verdadeira ou falsa, sendo portanto uma proposição.
“O João tem o carro à entrada do parque” (proposição atómica ou afirmação não decomponível) E “já colocou o cartão de pagamento” (proposição atómica ou afirmação não decomponível). Estas duas proposições atómicas combinadas pelo operador E (AND) constituem uma afirmação com resposta verdadeira para a abertura da cancela ou falsa para a manter fechada. São portanto uma proposição.
As afirmações contempladas numa proposição, podem até envolver fórmulas que exprimam relações entre várias afirmações estabelecidas com operadores lógicos, mas a sua resposta será sempre só uma de entre duas possíveis: verdadeira ou falsa.
As proposições representam então, as fórmulas da lógica proposicional ou cálculo proposicional.
Estamos agora em condições de poder apresentar a definição de Lógica proposicional ou Cálculo proposicional sem que ninguém se assuste:

    Cálculo Proposicional é um sistema no qual as fórmulas representam proposições que podem ser formadas pela combinação de proposições atómicas usando operadores lógicos.

Agora, para percebermos por que razão aqui aparecem introduzidos os temas lógica proposicional  e teoria dos conjuntos, temos que recuar no tempo e fazer um pouco de História.

Álgebra de Boole

Em 1854, o matemático britânico George Boole, através da obra intitulada “An Investigation of the Laws of Thought” (uma investigação sobre as leis do pensamento), apresentou um sistema matemático de análise lógica conhecido como álgebra de Boole.
A álgebra de Boole é uma teoria Matemática baseada em estruturas algébricas que capturam a essência das operações lógicas AND (E), OR (OU) e NOT (NÃO), bem como da teoria de conjuntos. Mais especificamente, a álgebra de boole foi uma tentativa de utilizar técnicas algébricas para lidar com expressões no cálculo proposicional.
Esperemos que já tenham entendido a importância do que o Sr George Boole fez. A álgebra Booleana foi desenvolvida com base nos mais antigos conceitos dos filósofos Gregos sobre a Lógica, como por exemplo o método de investigação de Sócrates, segundo o qual, “se duas verdades são alcançadas individualmente ao juntá-las tem-se uma única verdade”.
Portanto, George Boole criou estruturas algébricas que trabalhavam a dualidade verdadeiro/falso de afirmações através dos operadores lógicos, isto é, criou o que viria a ser o Cálculo proposicional ou Lógica proposicional.
George Boole, sem o saber e com cerca de um século de antecipação,  estava a criar o fundamento da matemática computacional, baseada em números binários.
As álgebras booleanas foram pela primeira vez aplicadas a interruptores por Claude Shannon, no século XX, que demonstrou que a aplicação a circuitos elétricos da álgebra de Boole podia resolver qualquer relação lógica e numérica.
Uma variável Booleana pode assumir apenas dois valores: 1 e 0, ou verdadeiro e falso, como por exemplo:

• A lâmpada está acesa (verdadeiro) ou a lâmpada está apagada (falso) se a lâmpada estiver acesa.
• Uma porta está fechada (verdadeiro) ou uma porta está aberta (falso) se a porta estiver fechada.
• Um interruptor está aberto (verdadeiro) ou um interruptor está fechado (falso) se o interruptor estiver aberto.

E a sua representação pode ser feita por:

• Símbolos (Portas Lógicas). A porta Lógica é a aplicação do conceito de operador lógico a algo com representação física que se pode inserir num circuito lógico.
• Expressões algébricas lógicas.
• Tabelas verdade,  que consistem de tabelas com o valor da saída para todas as combinações possíveis dos valores das entradas.

Operadores Lógicos

Bom, já falámos aqui várias vezes em operadores lógicos e ainda não os definimos. A sua definição tem que ser feita com tempo e espaço, para que sejam bem entendidos. Certamente já perceberam que o segredo das tais capacidades do computador vai passar por aí.

Para definirmos os operadores lógicos vamos analisar um conjunto de objetos utilizando os conceitos da lógica proposicional, construindo proposições que vão assumir os estados de verdadeiras ou falsas conforme o objeto e  a propriedade em análise, definindo assim a que conjunto pertence cada objeto e o conteúdo de cada conjunto depois de analisar todos os objetos.
Por exemplo a proposição “É do sexo masculino” E “Tem mais de 20 anos” tem duas proposições atómicas que vão devolver verdade quando estivermos a analisar se o objeto é do sexo masculino e se tem mais de 20 anos.

As propriedades que vamos utilizar para analisar os objetos são:
a – ser maior de 20 anos .
b – ser do sexo masculino.
Os objetos que vão ser analisados sob a perspetiva destas propriedades são os clientes da“Noites Felizes”, que assim se vão tornar membros dos conjuntos A ou B, conforme as proposições que definem as qualidades de cada cliente relativamente às propriedades a ou b devolverem verdadeiro.
Por exemplo, a proposição “O António tem 18 anos”, é decomponível em duas proposições atómicas que devolvem verdadeiro para a propriedade b (“O António” – é do sexo masculino) e falso para a propriedade a (“tem 18 anos” – tem menos de 20 anos), pelo que ele tem a qualidade que lhe confere a pertença ao conjunto B mas não ao conjunto A.
Quisemos deixar bem clara a diferença entre as variáveis a e b, que definem qualidades  específicas de cada cliente e que farão parte das proposições a analisar e os conjuntos A e B que serão compostos, cada um, pelo conjunto de objetos (clientes) para os quais as proposições devolverem verdadeiro.

Como forma de sermos mais objetivos na análise vamos focar-nos na  situação concreta de quatro clientes da “Noites Felizes”:

• O João (b), com 32 anos (a):
  a é verdadeiro, portanto a=1.
  b é verdadeiro, portanto b=1.

• A Isabel (b), com 25 anos (a):
  a é verdadeiro, portanto a=1.
  b é falso, portanto b=0.

• O Francisco (b), com 18 anos (a):
  a é falso, portanto a=0.
  b é verdadeiro, portanto b=1.

• A Tereza (b), com 18 anos (a):
  a é falso, portanto a=0.
  b é falso, portanto b=0.

Vamos também tentar também imaginar uma situação de automatização de produção em que, sem intervenção humana e em função da informação que determinados dispositivos lhe fornecem, o computador toma uma decisão que aciona outros dispositivos. Vamos ver o caso do parqueamento que abordámos no início.

Mas no próximo artigo.