Subtração binária

Subtrair um número de outro não é mais do que adicionar-lhe o seu simétrico. Portanto se eu pretendo subtrair 37 de 65 obtenho o mesmo resultado se adicionar a 65 o simétrico de 37, isto é, (-37)

65 – (+37) = 65 + (-37) = 28

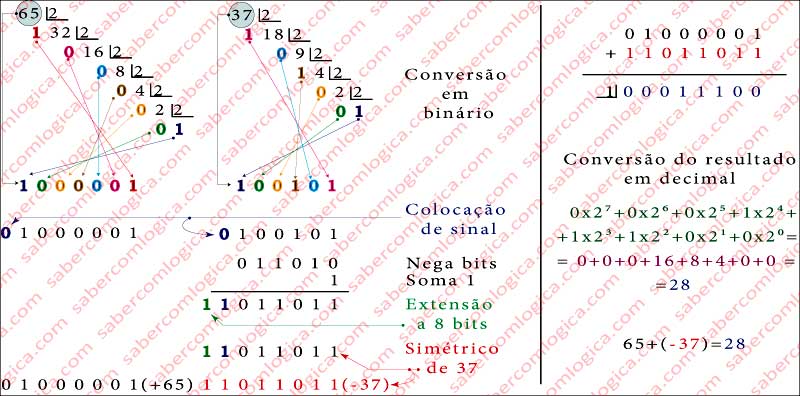
Ora, na base 2 tudo se passa da mesma maneira. Quando queremos subtrair um número a outro, determino o seu simétrico e fazemos uma soma. Então vamos lá experimentar fazer a operação acima indicada, em binário, exemplificada em gráfico na  Figura 1. Primeiro vamos converter os números 65 e 37 para a sua representação binária sem sinal. O número 65, agora 1000001 é representado por 7 bits. Acrescentando-lhe o sinal 0 pois é positivo passará a ter 8 bits, estando assim preparado para a operação como

65 = 01000001

Com o número 37, agora 100101 teremos muito mais coisas para fazer. Acrescentando-lhe o sinal 0 pois é positivo passará a ter 7 bits, como 0100101. Então negamos o bits e adicionamos 1 ao resultado, chegando a 1011011. Finalmente estendemo-lo a 8 bits, ficando assim preparado para a operação como

(-37) = 11011011

Podemos então agora fazer a soma de 65 e (-37) em binário, conforme se vê na Figura 1. O carry out final da operação tem o valor 1, mas como não cabe numa representação a 8 bits é ignorado. Como dissemos já vamos tratar desta questão.

Afinal, soma e subtração tratam-se da mesma operação, só que com pressupostos diferentes.

Será que é possível identificar um padrão de comportamento nas duas operações que nos permita, com a introdução de alguma lógica adicional ao circuito somador, fazer com que um mesmo circuito sirva os dois propósitos?

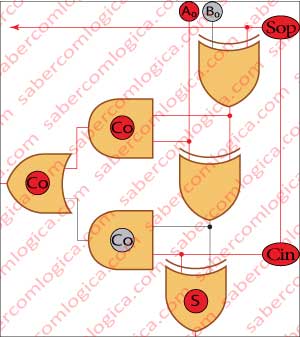
Vamos lá a ver acompanhando com a Figura 2, que ilustra a materialização deste circuito. Em primeiro lugar temos que fazer chegar ao circuito a informação sobre o tipo de operação que ele deverá efetuar, se é de soma ou de subtração. Isso consegue-se utilizando um sinal de controlo a que vamos chamar Sop (Sinal da operação).
Caso se trate de uma subtração vamos ter que negar os bits do segundo operando, mas só nesse caso, o que já nos vai obrigar a pensar um pouco.

Como é que vamos dizer ao circuito se nega ou não os bits do segundo operando? Sim, porque estamos a falar de mesmo um circuito que faz as duas operações.

Talvez não seja assim tão difícil. Para negar os bits vamos usar a porta lógica que, como já vimos,  faz isso por nós. É a porta XOR. Sempre 1 quando diferentes e 0 quando iguais. Vamos colocar uma porta XOR por cada bit antes do circuito somador, ligando a uma das suas entradas o bit do segundo operando e à outra o sinal identificador da operação Sop. Desde que Sop tenha o valor lógico 1, como é o caso da subtração, o operador XOR cumpre a função e inverte o valor de todos (nega) os bits do segundo operando.

Então e se for uma soma?

Nesse caso, desde que Sop tenha o valor 0 indicando soma, essa entrada da porta XOR terá o valor 0 e devolve um valor sempre igual ao do bit do segundo operando, que está na sua outra entrada, não invertendo (não negando) os seus bits. Se ligarmos a saída desta porta XOR à entrada do segundo operando no circuito somador, a negação dos bits em caso de subtração e só neste caso está resolvida.

Pois! Mas o que tem que lá estar não é a negação mas sim o simétrico. E para isso falta somar 1 à negação. E agora?

Temos que somar 1 ao primeiro bit!

Mas já estamos a somar os dois bits de ordem zero dos operandos, como é que vamos lá colocar mais um bit?

Talvez se, em vez de um circuito somador parcial para o primeiro bit usarmos um circuito somador completo. Aí já podemos introduzir mais um elemento à soma, sob a forma de um carry in. Pois, até aqui tudo certo.

E como é que vamos informar o nosso amigo que só usa esse valor quando se tratar de uma subtração?

Espera! Não lhe dizemos nada disso. Ele soma sempre o valor do carry in. Esse valor é que pode ser 1 ou 0. Então basta ligá-lo ao Sop, o sinal da operação, e assim o primeiro carry in do circuito (Cin) assumirá o valor 1 se for subtração ou o valor 0 se for soma.

Agora sim. Já está. Está garantido que o segundo operando será sempre representado pelo seu simétrico em caso de subtração.

Vamos lá juntar as pontas disto tudo e resumir:

• Devemos então ligar a cada uma das entradas do segundo operando do circuito somador, a saída de uma porta lógica XOR cujas entradas são Sop e o respetivo bit do segundo operando.
• Se o sinal da operação (Sop) for 0 nada se passa e o bit fica igual. Se o sinal for 1 faz a negação do bit.
• Esse mesmo sinal deve chegar à entrada carry in (Cin) do circuito somador do primeiro bit, um somador completo, acabando assim a operação de cálculo do simétrico.
• Se o sinal de controlo for 0, nada acontece aos bits nem é adicionado nada porque o carry in é 0.

Era isto mesmo que se pretendia. Quando a operação for uma subtração os bits do segundo operando são negados e é-lhe adicionado 1, sendo portanto convertido no seu simétrico. Quando a operação for uma adição o segundo operando é utilizado tal como está.

Vamos fazer alguns gráficos deste circuito, ilustrando as várias operações de soma e subtração entre 5 e 13, tentando abranger  a soma e subtração de operandos com sinais iguais e sinais diferentes, o que se pode ver na Figura 4 em diversos Quadros.
Para certas operações com 5 e 13 em complemento para 2, como por exemplo a soma 13+5=18, precisamos de 6 bits (-32 a 31) para representar o resultado.

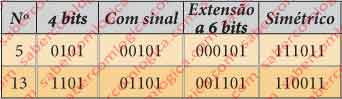
Também os números 13 e 5 para os quais bastam 4 bits na representação sem sinal, precisam de mais um bit, o sinal, para a sua representação em complemento para 2, portanto 5 bits.
Assim, vamos utilizar circuitos de 6 bits e estender a representação binária de 5 e 13 a 6 bits, como está representado na tabela da Figura 3.

Algumas observações importantes sobre os quadros da Figura 4 antes de prosseguirmos:

• Sop é o Sinal da operação (soma ou subtração), aquele que comanda o que se vai fazer com os operandos.
• Cin é o valor do Carry in no circuito somador do bit de ordem 0, cujo valor é igual ao do Sop.
• Os operandos A e B são representados pelos bits:
  •  A0 a A4 e SinA no lugar de A5 e
  • B0 a B4 e SinB no lugar de B5, respetivamente.
• SinA e SinB são os sinais de A e B, respetivamente.
• C0 a C5 representam os carry out dos circuitos somadores dos bits 0 a 5, respetivamente.
• S0 a S4 e Sinal no lugar de S5 representam o resultado, sendo que sinal é o sinal do mesmo.

Vamos então analisar os diversos Quadros da Figura 4.

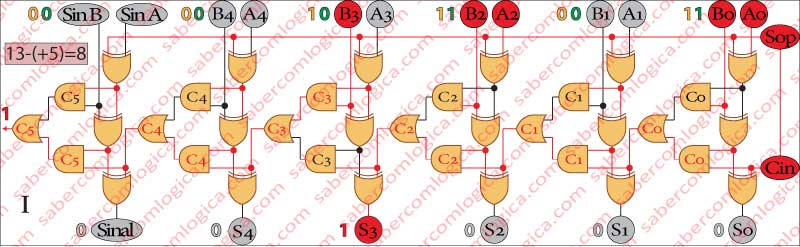
No Quadro I  da Figura 4 subtraímos (+5) de (+13).

Esta operação corresponde à subtração (Sop = 1) de operandos de sinal igual [(+13)-(+5)].

Na realidade, a operação que o circuito faz é uma soma. Informado pelo sinal Sop (1) que se trata de uma subtração, o segundo operando é convertido no seu simétrico e a operação que o circuito somador realiza é

[(+13)+(-5)].

O  resultado é 001000, ou (+8) em decimal.

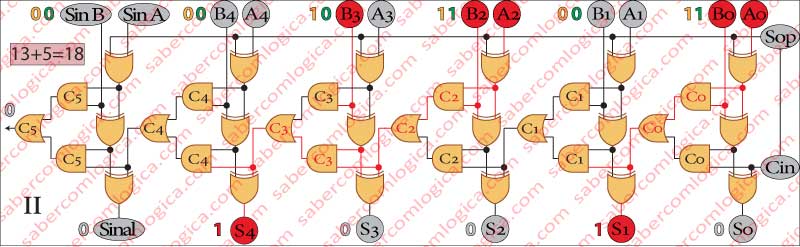
No Quadro II da Figura 4 somamos (+13) com (+5).

Esta operação corresponde à soma (Sop = 0) de operandos com sinal igual [(+13)+(+5)].

A operação que o circuito somador efetua é exatamente a identificada. Informado pelo sinal Sop (0) de que se trata de um adição, deixa passar o segundo operando sem qualquer alteração e executa a operação

[(+13)+(+5)].

O resultado é 010010, ou (+18) em decimal.

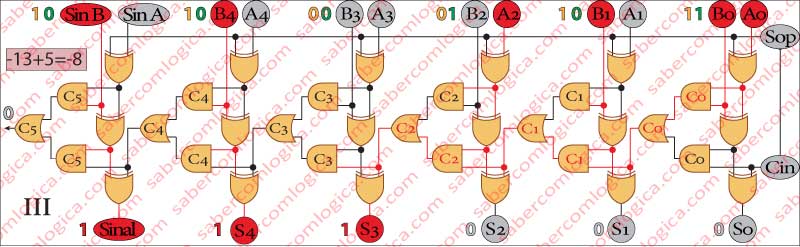
No Quadro III da Figura 4 somamos (+5) a (-13) .

Esta operação corresponde à soma (Sop = 0) de operandos com sinal diferente [(-13)+(+5)].

Informado pelo sinal Sop (0) de que se trata de uma adição, o valor do segundo operando passa sem qualquer alteração e a operação executada é

[(-13)+(+5)].

O resultado é 111000, ou (-8) em decimal.

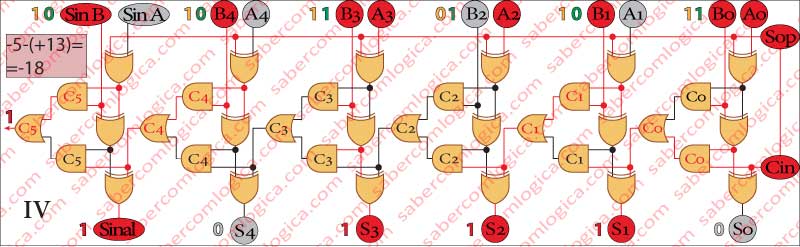
No Quadro IV da Figura 4 subtraímos (+13) a (-5).

Esta operação correspondente à subtração (Sop = 1) de operandos com sinal diferente [(-5)-(+13)].

Informado pelo sinal Sop (1) de que se trata de uma subtração, o segundo operando é transformado n o seu simétrico e a operação executada é

[(-5)+(-13)].

O resultado é 101110, ou (-18) em decimal.

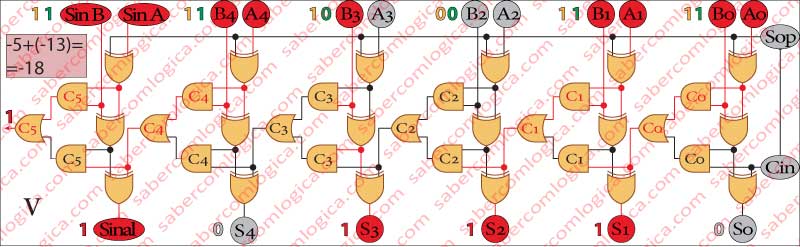
No Quadro V da Figura 4 somamos (-13) a (-5).

Esta operação correspondente à soma (Sop = 0) de operandos com sinal igual [(-5)+(-13)].

Informado pelo sinal Sop (0) de que se trata de uma soma, o valor do segundo operando passa sem qualquer alteração e a operação executada é

[(-5)+(-13)],

o que corresponde rigorosamente ao mesmo que fizemos no Quadro anterior, só que neste caso o sinal de operação indica soma e o segundo operando é negativo. A intenção foi somente permitir a visualização da diferença no circuito entre as duas situações. O resultado é 101110, ou (-18) em decimal.

Verificada a conformidade do circuito nestas situações de soma e subtração, com as quais pretendemos ilustrar como funciona a introdução dos operandos, o seu sinal  e a influência do valor de Sop sobre o segundo operando A, vamos então abordar o tema já por várias vezes referido, o Excesso.

O excesso  verificar-se-ia em duas das situações descritas por estes quadros, mais concretamente as dos quadros II e IV. Se não tivéssemos estendido a representação dos números a 6 bits, não existindo portanto o bit de ordem 5 para absorver esse excesso, a situação gerada provocaria um erro.

Repare-se no Quadro II. O carry out final do circuito é 1, certo? Mas ignorámos esse carry out. Porquê? No entanto dissemos que houve excesso absorvido pelo bit de ordem 5 e o carry out era 0. Como é então? Ignora-se quando é 1 e considera-se quando é 0?

Neste trabalho nós fazemos o que queremos. Porque sabíamos que o resultado da operação não cabia nos 5 bits estendemos o circuito a 6 bits.
Pois, mas na realidade, um circuito de 8 bits (p.e.) não é extensível, não sabe que operações vai fazer e muito menos o seu resultado. Mas tem que estar preparado para reagir corretamente perante todas as hipóteses em que for colocado, sempre prevenindo a possibilidade de erro.

É precisamente o que vamos ver na forma de tratamento de excesso em operações binárias. É uma questão demasiado importante para não ser abordada. A sua deteção é vital para que se proceda à sua correção ou se pare a execução do programa, sob pena de a partir daí se propagar um erro com consequências imprevisíveis.