A soma binária

Operações aritméticas? Mas ainda só falámos de portas lógicas com respostas verdadeiro ou falso. Como é que isso vai produzir somas, subtrações, multiplicações e divisões? Como é que é possível conseguir isso, utilizando combinações de portas lógicas em circuitos lógicos,  que refletem expressões da Lógica proposicional que só respondem verdadeiro ou falso?

Realmente, só com verdadeiro ou falso como entradas e saídas nos circuitos, não se consegue entender como se fazem somas de números tal como nós os conhecemos e tratamos, em representação decimal. Enquanto pensarmos como tal, em decimal. Mas no sistema numérico binário, talvez já não seja tão difícil de entender. Basta pensarmos que verdadeiro e falso se refletem em 1 e 0. Ora, como não há quaisquer outros números nesta base numérica, qualquer operação que envolva estes números só pode devolver 1 ou 0. E isso é precisamente o que fazem as portas lógicas.

Portanto, mais uma vez estamos a ser remetidos para uma questão de raciocínio lógico que conduza a combinações devidas dessas portas, para obter um objetivo. Vamos começar com o objetivo de somar, a origem de todas as outras operações. Mas para isso temos que aprender de novo a somar, isto é, vamos ter que decompor passo a passo aquilo que fazemos intuitivamente desde os primeiros anos de escola, para podermos determinar o algoritmo da soma. E agora vamos ter que o fazer com números binários, ou na base 2, começando por o fazer da forma mais intuitiva, tal como na escola, a papel e lápis, considerando exatamente os mesmos passos que aprendemos para a base 10.

Comecemos por somar dois números na base 10, a papel e lápis, sem máquina de calcular. Somemos por exemplo o número 76.354 com o número 32.377, acompanhando desde já com o desenvolvimento do algoritmo dessa soma.

1. Colocam-se os dois números um por cima do outro, casa a casa e ambos encostados à direita.
2. Somam-se os dígitos de cada casa a partir da direita para a esquerda.
3. Somam-se os dígitos da primeira coluna e inscreve-se ma mesma coluna por baixo.
4. Se o resultado da soma for superior a 9 coloca-se na mesma coluna por baixo o algarismo à direita do 1 e acrescenta-se o 1 por cima da coluna seguinte. Chamamos a isto o “vai 1”.
5. Se não há mais colunas salta para o passo 7.
6. Se há mais colunas volta-se ao passo 3.
7. Se Vem 1 coloca-se na coluna à esquerda do resultado. A soma está concluída

Este é o algoritmo da soma na base 10. O algoritmo de soma na base 2 é exatamente o mesmo, com a diferença de que temos só dois dígitos, 0 e 1

0 + 0 = 0, 1 + 0 = 1, 0 + 1 =  1 e  1 + 1  = 2

Alto! Mas 2 não existe na base 2. Tal como 10 não existe na base 10 como dígito.
A base representa o número de  dígitos usados para representar números nessa  base. Dez (0 a 9) na base 10, dois (0 a 1) na base 2 e dezasseis (0 a F) na base 16.
Dez (10) é o nome que damos na base decimal ao primeiro número para além dos algarismos da base, número esse a que na base 2 vamos chamar  um/zero (10).
De cada vez que se esgotam os dígitos que representam números numa base, pomos um 1 à esquerda e recomeçamos a contagem.

• Em decimal depois de 9 vem 10, depois de 99 vem 100, depois de 999 vem 1000, e assim por diante.
• Em binário depois de 1 vem 10, depois de 11 vem 100, depois de 111 vem 1000 e assim por diante.
• Em hexadecimal depois de F vem 10, depois de FF vem 100, depois de FFF vem 1000 e assim por diante.

Portanto, a partir de agora vamos deixar de pronunciar  10 como dez para passarmos a pronunciar como um/zero, 100 não como cem mas como um/zero/zero e assim por diante. Desta forma estaremos a usar a mesma designação para um número com o mesmo significado em todas as bases de numeração. Assim sendo, quando somamos 1 com 1 na base 2 temos como resultado 10 (um/zero). Colocamos o 0 como resultado dessa coluna e vai 1 no topo da coluna à esquerda. Vamos experimentar e somar 1011 com 1011, seguindo passo a passo o algoritmo atrás enunciado. Podemos verificar este algoritmo representado em gráficos para a base 10 e para a base 2 na Figura 1.

Mas o computador não sabe somar assim. Ele não andou connosco na escola em pequenino e a velha mestra não lhe ensinou as regras e mnemónicas que utilizamos nas somas. Ele é teimoso e burro e continua a insistir em só conhecer 0 e 1. Diz que lhe basta. E olhem que até tem razão, como vamos ver. Só que assim dá-nos um trabalhão para lhe ensinarmos o que queremos que ele faça.

Temos então que, uma vez levada à essência a forma como resolvemos o problema no mundo real (determinado o algoritmo do problema), montar um bom raciocínio lógico temperado com um pouco de imaginação, que nos permita encontrar nas propriedades das portas lógicas, a resposta à nossa questão.

Estamos a somar na base 2. Os operandos só podem ser números compostos por 0 ou 1, tal como as entradas das portas lógicas. E o resultado é sempre expresso em 0 ou 1, tal como as saídas das portas lógicas. Talvez esta constatação nos torne mais clara a possibilidade de encontrarmos a solução com combinações de portas lógicas.

Circuito Somador Parcial

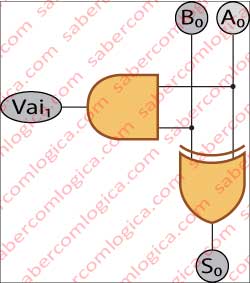
Relembramos agora ter dito há pouco que na base dois

0 + 0 = 0, 1 + 0 = 1, 0 + 1 =  1 e  1 + 1  = 0 e vai 1.

Ao revermos agora essa afirmação lembramo-nos da propriedade de uma porta lógica que responde sempre um dos dois mas não ambos, que é a disjunção exclusiva, ou eXclusiv OR ou XOR.

• Nas três primeiras hipóteses de soma (0+0=0, 0+1=1, 1+0=1) a resposta está certa. A porta XOR retorna na sua saída exatamente o valor correspondente ao resultado da soma.
• Na última (1+1=0 e vai 1) também está certa no dígito que fica nessa coluna, mas sobra a questão do vai 1. E a porta XOR não adivinha se vai ou não vai. Ela só sabe que se forem iguais a resposta é 0. Se forem diferentes a resposta é 1. Acompanhem com a Figura 2.

Partindo do principio que a solução pode passar pela utilização da porta XOR, continuemos então a pensar como podemos resolver a questão do vai 1. Ora, o vai 1 só se dá exclusivamente na situação em que A0 e B0 são 1. Nas restantes opções não vai nada. Fica-se por ali. Então, a resposta pretendida cai nas propriedades de uma porta AND. Basta pôr essa porta a analisar os mesmos dados em paralelo com a porta XOR.

Temos assim encontrada a composição para o circuito somador parcial ou do bit de ordem 0, em que o resultado da soma desses bits se encontra nas saídas S0 e C0.

Mas porquê parcial?

Recordemos que neste circuito existe o conceito do “vai um”. Ora a admissão da existência de um vai 1 implica que nos circuitos somadores dos bits de ordem seguinte tenha que ser considerado também o conceito do “vem um”. A esse circuito chamaremos circuito somador completo e vamos abordá-lo já de seguida. Mas antes de prosseguirmos vamos ter que fazer uma referência clarificadora dos  vai 1 e vem 1.

Carry Out e Carry In

Esta designação escolar do vai um e do vem um assume em linguagem informática a designação de carry out ou carry in. Na realidade o vai um e o vem um só são referidos quando na realidade vai ou vem mesmo 1. Mas em termos informáticos e nos circuitos lógicos temos que considerar sempre a possibilidade de existência desse valor, seja 1 ou 0 e isto de estar a dizer que vai um ou vem um quando não vai nem vem nada, não bate certo. Portanto os termos ingleses de carry in (transporta para dentro) ou carry out (transporta para fora) estão mais corretos no seu significado e por isso vamos adotá-los, sendo que:

•  Carry Out (Co)  é o valor que não cabe na representação da ordem de bits a ser somada e que é transportado para a soma dos bits de ordem imediatamente superior.
• Carry In (Ci) é o valor que não cabe na representação da ordem de bits imediatamente anterior e que é transportado para a soma dos bits a ser somada.

O Somador Completo

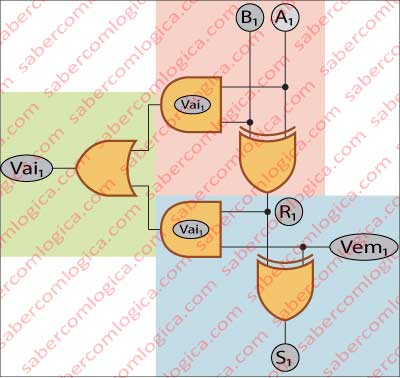
Referimos que num circuito somador de um bit de ordem superior a 0 teríamos que considerar a existência de um vem um, ou antes de um Carry In (Ci)
Ora, em termos práticos isto corresponde a termos que somar o Carry Out (Co) do bit de ordem anterior (que é o Ci deste circuito) em conjunto com os bits deste circuito.

Mas a solução que encontrámos só consegue somar dois bits de cada vez. Como vamos incluir o terceiro bit?

Vamos somar primeiro os dois bits A1 e B1 desta ordem e chamar ao resultado R1. Depois somamos o resultado R1 com o Ci. Para isso colocamos um segundo somador parcial que tem com entradas R1 e Ci. Portanto temos dois circuitos somadores parciais em série. Ora cada um deles tem um Co, portanto o circuito somador desta ordem de bit vai ter dois Co.

Mas não pode ter dois Co. Então como é que isso se faz?

Não pode, evidentemente, porque o seguinte só pode ter um Ci. Assim sendo, temos que tratar os dois Co de forma a que o circuito só tenha um.
Vamos acompanhar com a Figura 3 onde, com fundo rosa temos o primeiro circuito somador, com fundo azul o segundo circuito somador e com fundo verde o tratamento dos dois Co. Nesta Figura também apresentamos o funcionamento físico do circuito de soma completo, para que possam seguir o comportamento dos transístores conforme o valor das entradas muda.

Indo à essência da operação, torna-se fácil verificar que, se o Co do primeiro circuito for 1 o R1 é 0. Com efeito, o vai um só é digno do seu nome quando se soma 1 com 1, caso em que o resultado é 0 e vai 1. Então o R1 é 0 se o seu Co for 1. Assim sendo a soma de R1 com qualquer valor que venha em Ci dará obrigatoriamente um Co=0. Portanto, se o primeiro Co for 1, o segundo será 0. Se o primeiro for 0 o segundo pode ter qualquer valor, dependendo de R1 e de Ci.

Podemos então concluir que os dois Co ou são ambos 0, ou 0 e 1. Nunca ambos 1. E que o Co resultante dos dois será 1 se algum deles for 1 e 0 se ambos forem 0.

Ora, este tipo de resultado obtém-se aplicando um operador OR ao resultado dos dois Co. Devolve 1 se forem diferentes e 0 se forem ambos 0. A situação de ambos 1 não caberia no contexto desta porta, mas como nunca se pode verificar, a porta OR cumpre o objetivo. Será esta porta que dará o Co para o circuito seguinte ou para o fim da soma.

Já está. Encontrámos a composição de um circuito somador completo ou de bits de ordem superior a zero e também a forma como um computador soma.

Temos vindo a referir-nos insistentemente à ordem dos bits, por isso achamos oportuno fazer um esclarecimento sobre o que é a ordem de um bit, para que não se gere uma grande confusão em torno da questão.

A Ordem dos Bits

É uma afirmação que já fizemos por várias vezes durante este Capítulo. Os bits de ordem x, os bits de ordem superior, os bits de ordem inferior, etc. Os bits são os dígitos de um número binário representado pelo Byte ou pela Palavra. Num sistema de numeração posicional os dígitos têm o seu valor conforme a posição que ocupam no número. É a esta posição que chamamos ordem. A posição dos dígitos começa pela ordem 0 para o primeiro dígito à direita no número e cresce em ordem conforme vamos avançando nos dígitos para a esquerda no número.

Num Byte os bits começam pelo bit de ordem 0 ou pelo bit menos representativo e vão crescendo em ordem até chegarmos ao bit de ordem 7 ou bit mais representativo. Certamente repararam que não comparámos a ordem dos bits com a sua posição mais à esquerda ou mais à direita no Byte, tal como fizemos com os dígitos no número, e isso não foi por acaso. Normalmente quando se representa um Byte é com os seus bits crescendo da direita para a esquerda, mas não tem que ser obrigatoriamente assim. Por essa razão os bits de um Byte são representados por uma letra seguida de um número, número esse que representa a ordem do bit dentro do Byte, o seu grau de representatividade ou o seu peso (qualquer destas designações pode ser usada). X7 X6 X5 X4 X3 X2 X1 X0  representa um Byte com os seus bits, mas  X0 X1 X2 X3 X4 X5 X6 X7  representa exatamente o mesmo Byte.

Referimo-nos a este pormenor pois iremos encontrar durante este trabalho representações de Bytes com os bits alinhados da esquerda para a direita, da direita para a esquerda, de baixo para cima ou de cima para baixo, conforme a posição do componente onde o Byte e os seus bits são representados. Por esta razão a ordem do bit no Byte é sempre indicada pelo número depois da letra. E é esta indicação que prevalece, não a sua posição. Referimo-nos ao Byte mas o mesmo aplica-se a qualquer Palavra de qualquer tamanho.

Circuito somador de 4 bits

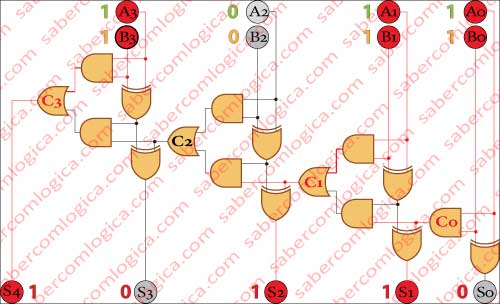
Toda a análise que fizemos foi só para um bit. Primeiro para o de ordem 0 e depois para o de ordem 1. Por isso juntamos agora um gráfico, na Figura 4 com a soma de dois números de 4 bits, exatamente os mesmos que usámos antes, a papel e lápis. Aqui pode-se ver o funcionamento conjunto dos circuitos parciais e completos de soma. Neste circuito não nomeámos os valores transportados por Ci ou Co mas simplesmente por C (Carry) com a um número indicativo da ordem do bit que o originou. Na realidade, neste circuito carry in e carry out são o mesmo, dependendo só do lado de que são olhados ( do que o recebe ou do que o produz).

Agora experimentem substituir os operandos por outros valores, analisem o comportamento das portas lógicas face às entradas, obtenham o resultado final e comparem com o que seria em decimal, para verificarem se estão certos.

Chegámos até aqui por deduções lógicas, combinando as diversas portas lógicas usando somente formas lógicas de associação das mesmas, como dissemos que faríamos. Agora vamos encontrar as expressões algébricas Booleanas da soma de dois números de 2 bits. Escolhemos 2 bits, os dois primeiros bits do circuito, porque assim apanhamos um circuito somador parcial e um circuito somador completo. De notar que, para cada bit de saída de um circuito existe uma expressão algébrica booleana. Então teremos:

S0 = A0 XOR B0 ou A0⊕B0 ou NOT (NOT (A OR B) OR (A AND B)) ou ¬(¬(A+B)+(A.B))
C0 = A0 AND B0 ou A0∙B0
S1 = (A1 XOR B1) XOR C0 ou (A1⊕B1)⊕C0 ou NOT (NOT (NOT (NOT (A1 OR B1) OR (A1 AND B1)) OR (A0 AND B0)) OR (NOT (NOT (A1 OR B1) OR (A1 AND B1)) AND (A0 AND B0))) ou ¬(¬(¬(¬(A1+B)1+(A1∙B1))+(A0∙B0))+(¬(¬(A1+B1)+(A1∙B1))∙(A0∙B0)))
C1 = (A1 AND B1) OR ((A1 XOR B1) AND C0) ou (A1∙B1)+((A1⊕B1)∙C0) ou (A1∙B1)+((NOT (NOT (A1 OR B1) OR (A1 AND B1)))∙(A0∙B0)) ou (A1∙B1)+((¬(¬(A1+B)1+(A1∙B1))∙(A0∙B0))
S2 = C1

O resultado final é representado pelo número binário   S2 S1 S0 e o seu valor decimal será  S0 x 2°+ S1 x 2¹+ S2 x 2². Na Figura 5 encontra-se descrita a operação tal como seria executada à mão.

Observação:

Devem ter reparado que vimos a apresentar as expressões algébricas booleanas de todos os circuitos que temos analisado. Também têm certamente verificado que as expressões se têm tornado mais complexas conforme a complexidade dos circuitos tem crescido. Vejam esta última por exemplo. Agora substituam S2 S1 S0 pelas suas expressões algébricas booleanas. É uma enormidade e estamos a falar de uma soma de dois bits. Claro que estas expressões têm que ser simplificadas pelas regras e teoremas da Álgebra de Boole e por métodos empíricos, como os mapas de Karnaugh, p.e. o que não está no âmbito deste trabalho.

Daqui em diante não vamos colocar mais expressões. Vamos deixar esta questão para o local próprio, um provável Capítulo que gostaríamos de escrever sobre Lógica Matemática. Para já a intenção foi só uma tentativa de abordagem a essa forma de representação matemática.