Circuitos de seleção e descodificação
Para avançarmos na Lógica do computador há alguns conhecimentos que devemos adquirir antes. A CPU é constituída pela interação de circuitos lógicos que agora vamos ver, integrados no seu próprio circuito. Operações aritméticas que tenham que ser executadas por métodos iterativos, também utilizam a interação destes circuitos. O Multiplexer ou MUX, o Demultiplexer ou DEMUX como exemplos de cicuitos de seleção e o Descodificador são circuitos que vamos analizar neste artigo.
Todos os circuitos que vamos analisar são conseguidos por combinações das portas lógicas NOT, NAND, NOR, AND, OR, XOR and XNOR.
O MULTIPLEXER
O QUE FAZ
O Multiplexer (MUX) pode selecionar uma de várias entradas através de combinações de bits de seleção. Para cada combinação dos bits de seleção, uma entrada é selecionada.
Assim, 1 bit seleciona 1 de 2 entradas, 2 bits selecionam 1 de 4 entradas, …, 16 bits selecionam 1 de 256 entradas, …, N bits selecionam 1 de 2N entradas. Como podemos verificar, o número de entradas que um MUX pode selecionar está relacionado com o número de possíveis combinações dos bits de seleção. Por exemplo, com 32 bits, podemos selecionar1 de 232, ou 4,294,967,296 entradas.
E para que serve um circuito destes?
Se a vossa imaginação não estiver ainda a voar, vamos dar-lhe um pouco de energia. Imaginem por exemplo que querem selecionar um célula de memória de entre milhares de milhões. Não será útil para isso?
Agora vamos supor que queremos escolher entre dois valores que vêm de circuitos diferentes, sob a condição de uma determinada circunstância ser ou não verificada. Ora isto é uma decisão condicional que vamos ter que tomar com base nas ditas circunstâncias. E a análise à condição retornará um valor lógico verdadeiro/falso, o tal bit de seleção, encontrado algures noutro circuito e condicionando a escolha do MUX. Esta situação será encontrada, por exemplo, quando analisarmos a CPU.
Agora vamos ver o caso de uma abstração, um programa de computador, que contém frequentes decisões condicionais expressas em instruções como.
if (condicão) FAZ ISTO else FAZ AQUILO
que deve ser lido como o é em Inglês.
A condição pode ser o resultado da análise a expressões proposicionais envolvendo quantificadores e comparadores, portanto valores humanos devolvendo um valor verdadeiro/falso, 1 ou 0, precisamente bit de seleção que fará o MUX escolher entre o FAZ ISTO se verdadeiro (1) ou o FAZ AQUILO se falso (0), as entradas do MUX .
Quando analisamos condições como x>0, ou x>o AND x<10, ou O homem pesa 80 kg, ou O homem pesa mais de 80 kg AND tem mais de 1.80 mt de altura, estamos a fazer cálculo proposicional e predicativo. Estamos a analisar proposições que envolvem quantificadores e comparadores humanos, devolvendo exclusivamente verdadeiro ou falso, 1 ou 0, portanto um valor booleano, um valor para o computador.
Um programa de computador é uma abstração que se materializa nos circuitos do computador para ser executada, como a simples e básica relação anterior demonstra. E, como sempre, a complexidade não é mais do que a soma das mais elementares simplicidades.
Generalizando, podemos dizer que o MUX tem a simples função de, em qualquer momento selecionar um de entre vários possíveis valores de acordo com os valores dos bits de seleção que recebe.
Como é que o faz
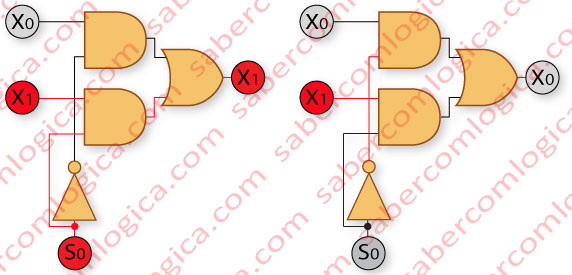
Na Figura 1, podemos ver um MUX com um bit de seleção S0 e duas entradas entradas para selecionar, X0 e X1.
Cada entrada está ligada a uma porta AND em conjunto com o bit de seleção.
Uma porta AND devolve 1 se ambas as entradas forem 1, de outra forma devolvendo 0. Portanto, a porta AND onde o bit de seleção tiver o valor 1, devolve 1, se a outra entrada for 1, e devolve 0 se a outra entrada for 0.
Por outras palavras, a porta AND onde o bit de seleção assumir o valor 1 devolve o valor da outra entrada, 0 or 1.
Tendo isto em mente, se quisermos selecionar X0 quando S0=0,devemos ligar a negação de S0 à mesma porta que X0. desta forma, quando S0 for 0, ¬S0 será 1 e o valo de X0 estará na saída dessa porta AND.
Da mesma forma, se quisermos selecionar X1 qaundo S0 for 1, devemos ligar S0 a mesma porta AND que X1. Assim, quando S0 for 1 teremos o valor de X1 vna saída dessa porta AND.
Portanto, só temos que fazer S0 ou ¬S0 assumirem o valor 1 na mesma porta AND onde a entrada, X0 or X1, que pretendemos selecionar está.
Quando S0 for 1, seja qual for o valor de X0 a sua porta AND evolve 0. Quando S0 for 0, seja qual for o valor de X1 a sua porta AND devolverá 0.
Dito isto podemos concluir que em cada momento só uma das portas AND está selecionada e tem na sua saída o valor da entrada correspondente, a porta AND onde o bit de seleção assume o valor 1.
Como o MUX só devolve um valor, se ligarmos as duas portas AND a uma porta OR asseguramos que o valor da entrada selecionada estará na saída de OR, seja 1 ou 0.
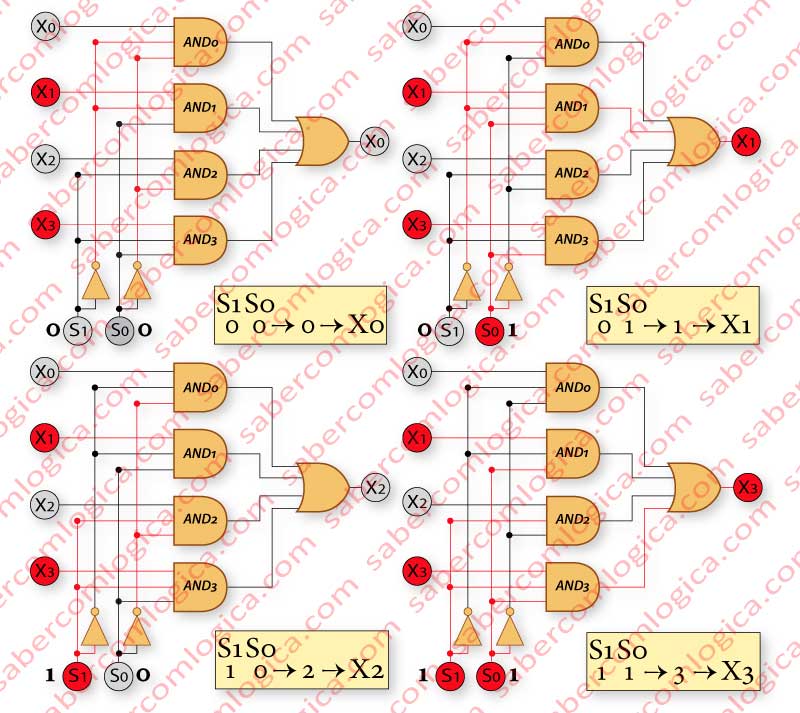
Mas um MUX pode selecionar de entre mais do que 2 entradas. Vamos analisar o caso de 4 entradas com 2 bits de seleção, como mostara a Figura 2. Os pressupostos essenciais serao os mesmos. Como agora temos dois bits de seleção as portas AND passarão a ter três entradas, duas para S0 e S1 e uma para X0, X1, X2 ou X3.
Figure 3
Os dois bits S0 and S1 têm 4 possíveis combinações (00, 01, 10 and 11), cada uma selecionando uma das 4 variáveis X0, X1, X2 ou X3, e devem ser ligados como segue:
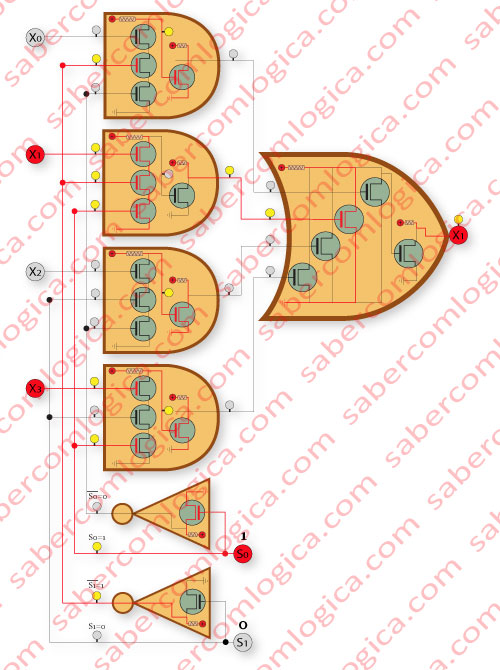
Figura 4
- Quando 00(0), selecionando X0, ¬S0 e ¬S1 a AND0.
- Quando 01(1), selecionando X1, ¬S0 e S1 a AND1.
- Quando 10(2), selecionando X2, S0 e ¬S1 a AND2.
- Quando 11(3), selecionando X3, S0 e S1 a AND3.
Desta forma a entrada selecionada será sempre a que tem a posição decimal indicada pelo valor decimal dos bits de seleção.
Como atrás, ligando todas as portas AND a uma porta OR garante-se que o valor da entrada selecionada estará na saída da porta OR
Na Figure 2 mostra-se graficamente como uma das 4 variáveis X0, X1, X2 or X3 é selecionada. As variáveis têm os valores X0=0, X1=1, X2=0 and X3=1.
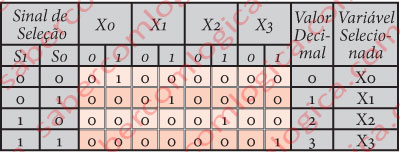
Na Figura 3 está representada a tabela verdade deste MUX e a correspondência entre o valor decimal dos bits de seleção e a ordem da saída selecionada.
Na Figure 4 em próxima página, pretende-se mostrar a materialização deste último circuito lógico.
O DEMULTIPLEXER
O Demultiplexer (DEMUX)coloca o valor de uma entrada em tantas saídas quantas as selecionáveis pelas combinações dos seus bits de seleção.
No que diz respeito à seleção das portas o seu funcionamento é idêntico ao do MUX. O valor da entrada é ligado a todas as portas de saída. Desta forma o valor da entrada estará sempre na porta selecionada, seja 1 ou 0.
Se não ligarmos nenhuma entrada ao DEMUX, isto é, se não existir uma entrada, então:
- A porta de saída selecionada terá sempre o valor 1 e todas as outras o valor 0, quando for um DEMUX com portas AND, portanto ativo a 1.
- A porta de saída selecionada terá sempre o valor 0 e todas as outras o valor 1, quando for um DEMUX com portas NAND, portanto ativo a 0.
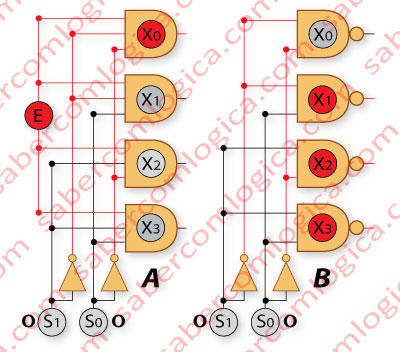
Na Figura 5 podemos ver o circuito lógico de um DEMUX 1 para 4 (1 entrada para 4 saídas) com portas AND (caso A) e com portas NAND (caso B).
O DEMUX com portas NAND não tem entrada, pois o nosso objetivo é mostrar que neste caso existe uma só saída (na porta selecionada) com o valor 0, como podemos verificar, sendo portanto um DEMUX ativo a 0.
Se o DEMUX com portas NAND tiver uma entrada E, ele inverte o seu valor na saída selecionada. Se E for 0 todas as saídas serão 1. Se E for 1 a saída selecionada será 0 e todas as outras 1. ¬E estará sempre na saída selecionada.
O Descodificador
O descodificador pode, com um conjunto de entradas (os bits de seleção) definir um subconjunto de saídas a partir de um muito maior conjunto de opções.
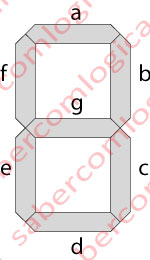
Cada dígito do ecrã é composto por 7 segmentos que podem ser iluminados individualmente. A cada momento é representado no ecrã o símbolo composto pelo conjunto de segmentos iluminados.
O número possível de combinações dos 7 segmentos é de 27 ou 128, isto é, podem ser representados 128 símbolos diferentes no ecrã. Mas o que nós pretendemos representar no ecrã são os 16 dígitos do sistema numérico hexadecimal.
Portanto, nós só queremos 16 de 128 possíveis símbolos, evidentemente só um ativo a cada momento.
Agora podemos seguir a descrição com a Figura 7. Se usarmos um DEMUX 1 para 16 sem entrada e com portas AND, podemos colocar o valor 1 na saída selecionada a partir das 16 existentes. E conseguimos fazer isto com 4 bits de seleção.
E cá está. Com um conjunto de 4 bits nós selecionamos um subconjunto de 16 símbolos a partir de um conjunto mais alargado de 128 possíveis símbolos. esta foi a definição inicial que pretendemos demonstrar com este exemplo prático. Está feito. Isto é um Descodificador.
O circuito lógico do nosso descodificador está dividido em duas secções.Na primeira secção temos um DEMUX com tantos bits de seleção quantos os necessários para selecionar um número de portas igual ao número de opções pretendidas para o subconjunto.
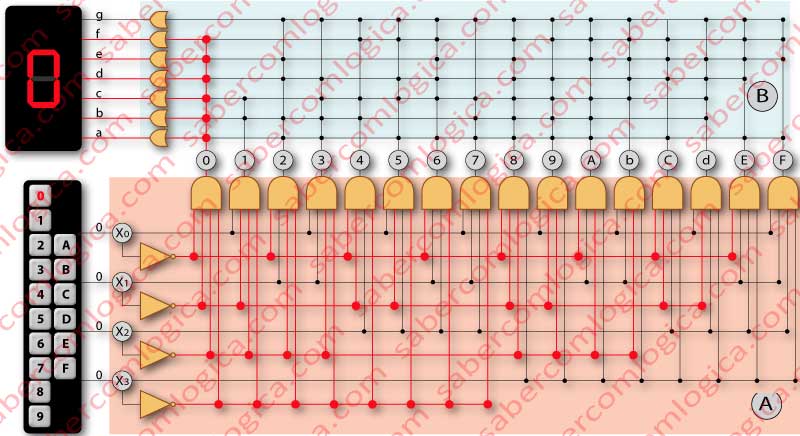
Na segunda secção temos um circuito mapeado em que as linhas que saem das portas AND do DEMUX são ligadas com as linhas que ligam aos segmentos a,b,c,d,e,f,g, isto é, cada linha de saída de uma porta AND liga com linhas para os segmentos que serão iluminados para formar o símbolo selecionado por essa porta.
Cada um dos segmentos do dígito está ligado com a saída de uma porta OR. À entrada de cada porta OR ligam as linhas mapeadas com as saídas do DEMUX que pretendem iluminar o segmento que lhe está ligado.
Podem existir até 16 linhas para cada porta OR, dependendo do número de saídas do DEMUX que queiram iluminar cada segmento. Na Figure 7 essas linhas são representadas por uma só, devido à evidente falta de espaço, embora na realidade a sua quantidade possa ir até 16, quando todas as saídas do DEMUX pretendem iluminar esse segmento.
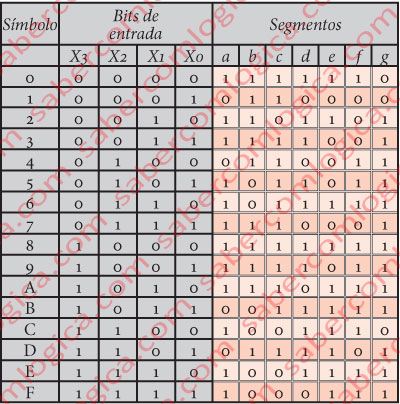
O mapeamento consiste no estabelecimento de ligações fixas entre as linhas que vêm do DEMUX e as linhas que vão para os segmentos de cada dígito de acordo com a tabela verdade deste descodificador, representada na Figure 8.
