A Divisão
Para conceber o circuito lógico que efetue a divisão entre dois operandos, vamos ter que entrar finalmente num campo de interligação de circuitos complexos mais elaborado do que os que até agora executámos.
Vamos decompor o desenvolvimento do raciocínio em três partes:
- Uma primeira, em que vamos olhar a divisão de dois binários sem sinal, feita a papel e lápis, determinar o seu algoritmo e inseri-lo no contexto dos componentes do circuito que vamos criar.
- Uma segunda, em que vamos desenvolver o esquema do circuito para a divisão em complemento para 2.
- Uma terceira, em que desenvolveremos vários quadros que representarão os componentes essenciais do circuito em que analisaremos a evolução dos valores nos mesmos ao longo das diversas iterações.
O Sinal da Operação
O que na realidade dividimos são os módulos dos números, i.e., sempre números positivos. O sinal da divisão é tratado mentalmente em separado. Se os sinais de divisor e dividendo forem iguais o quociente será positivo e se forem diferentes o quociente será negativo. O resto da divisão terá o mesmo sinal do dividendo. Assim sendo e seguindo aquilo que nós fazemos, no circuito da divisão de números em complemento para 2, vamos tratar o sinal separadamente através do bit de maior significado (o do sinal) e fazer a operação com o valor positivo de cada número.
Algoritmo da Divisão a Papel e Lápis
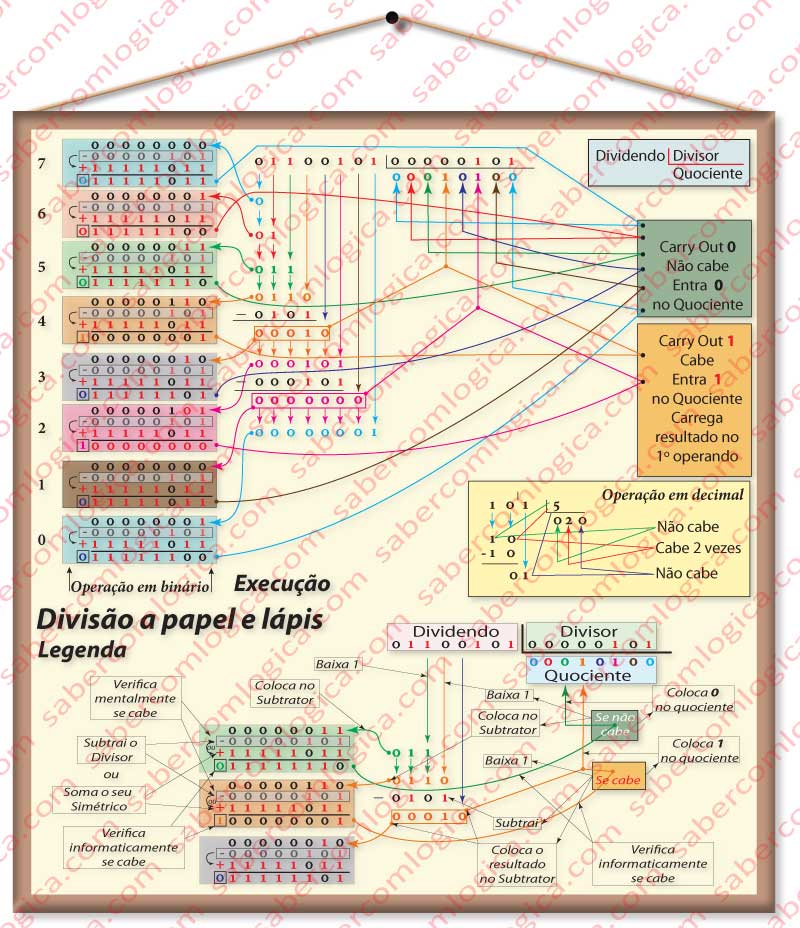
Na Figura 1 temos o quadro da velha sala de aulas onde a professora tem desenvolvido o algoritmo da divisão.
E é precisamente o mesmo que vamos fazer, só que com números binários e tomando as devidas conclusões para podermos ensinar o computador. E por isso vamos fazê-lo como ele, passo a passo, dígito a dígito, nunca usando as nossas capacidades mentais para juntar vários passos num só.
As linhas a cores tentam mostrar os caminhos do nosso raciocínio e são explicadas na legenda da figura. Os pequenos quadros da esquerda representam a subtração que se faz de cada vez que se baixa um dígito do dividendo, entre o valor resultante e o divisor. À esquerda de cada pequeno quadro está indicado o número da iteração. A subtração é convertida na soma com o simétrico, por uma questão de igualdade de procedimento com o circuito digital. É o valor do carry out desta soma que vai permitir ao computador determinar se cabe (1) ou não cabe (0). A seguir já vamos ver porquê. Os dois quadros da direita simbolizam a tomada de decisão em relação ao carry out.
Vamos então elaborar o algoritmo da divisão, descrevendo os passos para a sua concretização e deixando-o já preparado para o computador. Pode seguir estes passos acompanhando com a Figura 1 que, se for clicada ou tocada pode abrir noutra janela. Assim:
- Convertem-se ambos os operandos em positivos.
- Determina-se o sinal do resultado da operação através dos sinais dos operandos, sendo que + por + e – por – dá + e – por + e + por – dá –.
- Baixa o primeiro dígito à esquerda do dividendo.
- Na caixa à esquerda toma o lugar de 1º operando e é estendido a 8 bits.
- Salta para o passo 8.
- Baixa o dígito do dividendo imediatamente à direita do último que foi baixado.
- Na caixa à esquerda, desloca os dígitos para a esquerda e acrescenta à direita o dígito agora baixado.
Subtrai o divisor ao 1º operando. - Subtrai o divisor ao 1º operando.
- Se o carry out do resultado for 0, é porque o divisor não cabe no 1º operando, pois é maior do que ele. Salta para o passo 11.
- Se o carry out do resultado for 1, é porque o divisor cabe no 1º operando, pois é menor do que ele. O resultado da subtração é estendido a 8 bits e toma o lugar do 1º operando para a iteração seguinte na caixa à esquerda.
- Coloca no quociente, imediatamente à direita do último dígito, o valor do carry out do resultado, isto é, 1 se o divisor cabe no 1º operando ou 0 se não cabe.
- Se não houver mais dígitos do dividendo para baixar, salta para o passo 14.
- Salta para o passo 6.
- Atribui-se ao resto o sinal do dividendo.
- Atribui-se ao resultado o sinal calculado no passo 2.
- Termina a operação.
Está pronta a receita para uma divisão binária feita a papel e lápis mas já preparada para um computador.
Agora vamos ter que a ensinar ao computador e encontrar o tipo de circuitos que implementarão cada um dos passos. Mas não sem antes entendermos a questão falada do Carry Out.
O Carry Out de uma Subtração de Números Positivos
Quando analisámos o Excesso foi concluído que “Quando os operandos de uma subtração têm sinais iguais não há lugar a excesso”, mesmo que o Carry Out tivesse o valor 1, o que se viu poder acontecer. Vamos agora analisar, em que situações assume o valor 0 ou 1 e o que é que iso significa em cada caso.
Uma subtração entre dois números não é mais do que a soma do primeiro com o simétrico do segundo. Foi desta forma que a representámos nos pequenos quadros e é desta forma que o computador a vai tratar em circuitos.
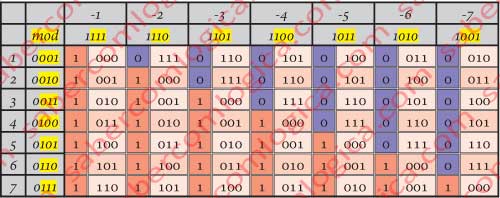
Vamos apoiar-nos na Tabela da Figura 2 para mais facilmente podermos entender a conclusão pretendida. Cada um dos quadrados de interceção dos números de 0001(1) a 0111(7), com o módulo do seu simétrico de 1111(-1) a 1001 (-7) o resultado da sua soma. Facilmente se verifica a linha de soma entre os simétricos, pois ela separa comportamentos diferentes do carry out.
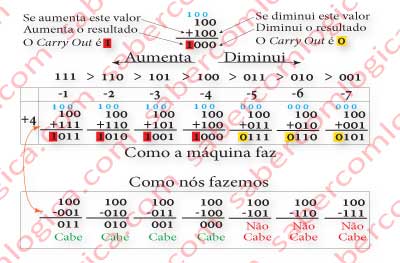
Recordemos que ambos os operandos são positivos antes da subtração, sendo o 2º operando substituído pelo seu simétrico parta a adição. Agora peguemos nos binários resultantes e na sua parte sem sinal e façamos a soma tal como na Figura 3. Como se pode ver a soma de um número com outro igual ou maior do que ele não é representável na mesma ordem de bits (carry out 1) e a soma de um número com outro menor do que ele próprio é representável na mesma ordem de bits (carry out 0).
Uma vez que a parte sem sinal da representação binária de números positivos cresce a partir de zero, como 100(4)>011(3)>010(2)>001(1) e a de números negativos decresce a partir de Zero, como 100(-4)<101(-3)<110(-2)<111(-1) podemos concluir que, sendo A o número positivo e B o número negativo:
- Quando o valor decimal de A é ≥ que o módulo do de B, a parte sem sinal da representação binária de A é ≤ que a de B, não sendo portanto a sua soma representável na mesma ordem de bits (carry out 1).
- Quando o valor decimal de A é < que o módulo do de B, a parte sem sinal da representação binária de A é > que a de B, sendo portanto a sua soma representável na mesma ordem de bits (carry out 0).
Então, falando em valores decimais e seus módulos, se A>B (B cabe em A), o carry out é 1 e se A<B (B não cabe em A) e o carry out é 0, podendo verificar-se que carry out 1→”cabe” e carry out 0→”não cabe“.
Componentes do Circuito Lógico
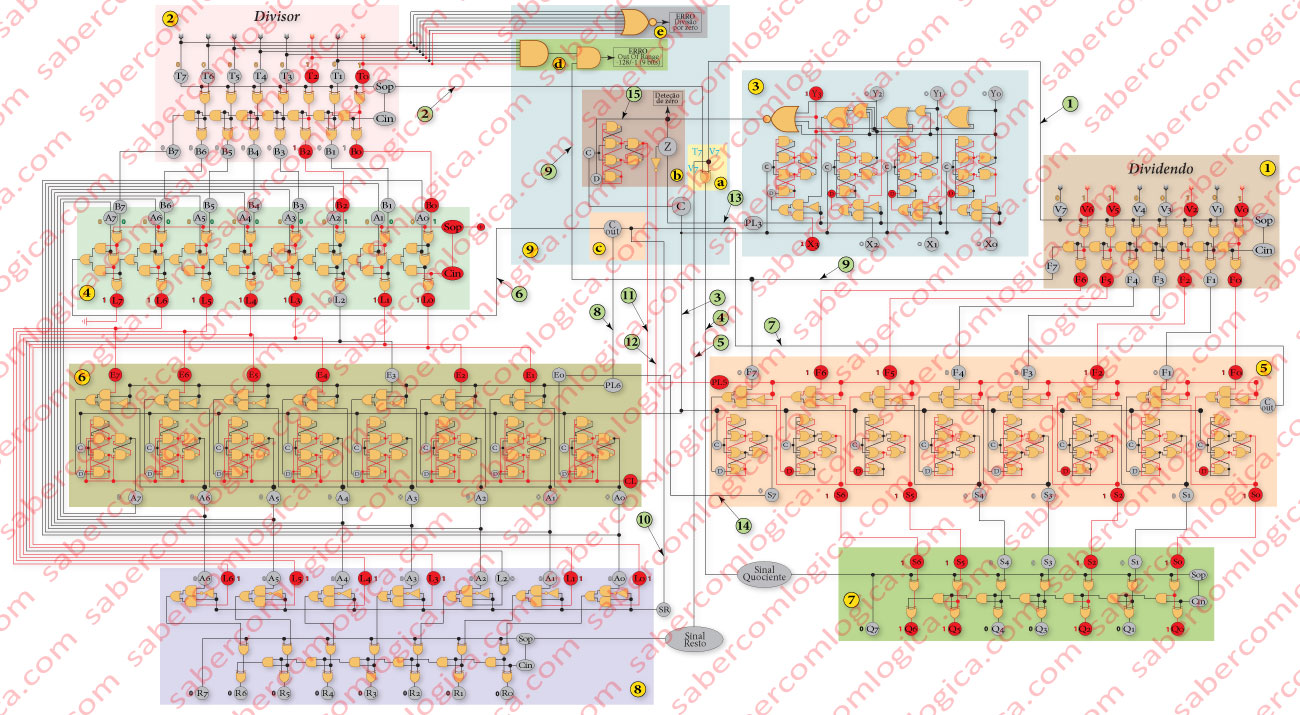
Na Figura 4 está representado um circuito de divisão para números de 8 bits em complemento para 2. Este circuito foi construído juntando diversos circuitos lógicos que achámos necessários para executarem os vários passos da operação. É um circuito imaginário onde qualquer comparação com a realidade é pura coincidência. Foi sendo construído conforme o íamos descrevendo. O nosso propósito foi, mais uma vez, o raciocínio lógico e a dedução lógica desta vez temporizada (clocked).
Para atingirmos o nosso propósito vamos começar por encontrar os componentes para executar os passos do algoritmo de entre os circuitos lógicos que já conhecemos, atribuindo cada um a cada passo. Podemos acompanhar a descrição com a Figura 4 e com a Figura 1 , clicando ou tocando nas imagens e abrindo-as em janelas diferentes.
No Passo 1 temos que “retirar o sinal e converter em positivos ambos os operandos”.
Cada um dos operandos vai ter que passar por um Circuito Conversor. O Dividendo pelo Circuito 1 e o Divisor pelo circuito 2. O que qualquer destes circuitos faz é, pela ação de Sop e Cin do respetivo operando, convertê-lo em positivo caso seja negativo. Digamos que é igual à parte de um circuito somador/subtrator, em que o Sop nega os bits e o Cin adiciona 1, caso o sinal do número seja negativo.
No Passo 2 do algoritmo temos que “determinar o sinal do resultado da operação através dos sinais dos operandos”.
Para a interpretação de diversos sinais do circuito e determinação do resultado da sua análise criámos uma Unidade de Controlo onde se inserem todos os pequenos circuitos de controlo. Vamos-lhe chamar Unidade de Controlo 9. Dentro desta Unidade de controlo cada circuito é identificado por uma letra. Para a pretensão deste passo do algoritmo vamos utilizar o Circuito 9a, que é simplesmente uma porta XOR a que ambos os sinais dos operandos estão ligados. Se forem iguais (+ por + ou – por –) a porta devolve 0 (dá +), se forem diferentes ( – por + e + por – ) a porta devolve 1 (dá –).
Nos Passos 3 e 6 do algoritmo “baixa-se um dígito do dividendo”.
Para este passo vamos utilizar um Registo de Deslocamento à esquerda com PL que será iniciado com o valor do dividendo. Por cada iteração este registo liberta um bit à esquerda, o tal dígito que se baixa. Vamos chamar-lhe Registo 5.
Nos Passos 4, 7 e 10 do algoritmo diz-se: “Na caixa à esquerda, coloca-se o 1º dígito baixado estendido a 8 bits (passo 1), ou desloca os dígitos para a esquerda e acrescenta à direita o dígito baixado (passo 2) ou o resultado da subtração estendido a 8 bits toma o lugar do 1º operando para a iteração seguinte na caixa à esquerda (passo 10)”.
Para todas estas tarefas vamos utilizar outro Registo de Deslocamento à esquerda com PL iniciado a zeros ficando assim o 1º bit baixado (o 1º a entrar) naturalmente estendido a 8 bits. O carregamento em paralelo acontece quando o quociente cabe e o valor do resultado da subtração é carregado neste Registo para a próxima iteração. Vamos-lhe chamar Registo 6. Conterá sempre o valor do 1º operando da operação de adição dos pequenos quadros do algoritmo. Os dígitos que vão entrando um a um no 1º operando (nos quadros à esquerda) portanto os que vão sendo admitidos neste Registo 6 são os que se vão baixando do dividendo, portanto os libertados com os deslocamentos à esquerda do Registo 5.
No Passo 8 do algoritmo “subtrai-se o divisor ao 1º operando”.
Para a execução deste passo vamos utilizar um Circuito Somador/Subtrator que simulará o comportamento das caixas da esquerda do algoritmo. Vamos chamar-lhe Somador 4. O 2º operando deste será o valor proveniente do Circuito 2, o Divisor. É aqui que se vai determinar o simétrico do valor já positivo e sem sinal do 2º operando, de acordo com o que vimos no parágrafo anterior (O Carry Out de uma Subtração de Números Positivos).
Por isso os sinais Sop e Cin neste circuito terão sempre o valor 1, não sendo dependentes do sinal de qualquer operando. Na realidade o valor que lá chega é sempre positivo, por ação do Circuito 2, tendo que ser convertido no seu simétrico para poder entrar na operação de adição. O 1º operando está permanentemente contido no Registo 6, pelo que será por ligação a partir deste que aqui chega. Este circuito fornece o resultado da operação e principalmente um carry out que será utilizado pelos Passos 9, 10 e 11 do algoritmo.
No Passo 11 do algoritmo “o valor do carry out é colocado no quociente no primeiro dígito à direita do último”.
Lá vem mais um registo de deslocamento à esquerda para os ir assumindo e deslocando à esquerda. Talvez não! Já temos um registo que liberta um bit à esquerda por cada iteração e vamos precisar de outro que assume um bit à direita por cada iteração. Então, o Registo 5 serve para as duas funções, concretamente para esta. Conforme vai largando valores do dividendo vai recebendo valores do quociente.
Nos Passos 9 e 10 do algoritmo “avalia-se o valor do carry out da soma e tomam-se decisões em função do seu valor. Em ambos os casos o seu valor corresponde ao bit a entrar no quociente. No caso de ser 1 o resultado da adição é carregado no 1º operando”.
Mais uma função para a unidade de controlo, desta vez no Circuito 9c, que encaminha o valor do carry out para o Registo 5, no qual vai entrar como dígito do quociente quando ele desloca os bits à esquerda, libertando o bit que baixa do dividendo. Encaminha o carry out também, para o Registo 6, onde vai através do PL provocar a carga do resultado da adição se o seu valor for 1.
No Passo 12 do algoritmo diz-se: “se não houver mais dígitos do dividendo para baixar”, ou por outras palavras, “se não houverem mais iterações para fazer…”.
Para podermos fazer esta afirmação vamos utilizar um Contador Decrescente com PL e Deteção de Zero. Carrega (PL) o número de iterações a efetuar, isto é, o número de dígitos do dividendo a baixar, começa a contagem decrescente, decrementando o seu valor por cada dígito baixado e por Clock e quando chegar a zero (Z) cumpre o que está escrito no algoritmo,isto é, salta para o passo 14. Vamos chamar-lhe Contador 3 e vamos fazê-lo ativo a 1.
No Passo 14 do algoritmo diz-se: “Atribui-se ao resto o sinal do dividendo”.
Tal como convertemos os operandos em positivos para determinar o valor da divisão, agora vamos ter que reconverter os resultados de acordo com o sinal determinado para eles. Neste caso, para o resto da divisão, é o sinal do dividendo. Para isso vamos usar um Circuito Inversor de Sinal a que vamos chamar Circuito 8. Para sabermos qual é o valor que deverá entrar neste circuito para ser convertido, vamos olhar para o último quadro do lado esquerdo do algoritmo. Podemos constatar que o resultado final do resto será o 1º operando, portanto o que está no Registo 6.
Pois é, mas parece que poderá não ser sempre assim!
Será assim se o divisor, na última iteração não couber no 1º operando, isto é se o carry out da operação for 0. Mas se couber, sendo o carry out 1, então a adição efetua-se e o resto será o resultado dessa operação, presente nas saídas do Somador 4, que não teve tempo (coitado) para entrar no Registo 6 antes do resultado ser lido.
Já de seguida vamos ver estas questões de propagação de sinais.
Então o resto pode ter valores provenientes de dois locais diferentes, conforme o valor do carry out. Daí a existência de um MUX de 2 para 1 neste Circuito 8. Cada uma destas duas possíveis resultados está ligado a um das entradas do MUX e o bit de seleção é o valor do carry out que para aqui é encaminhado pelo Circuito 9c. O valor do sinal do resto, que vem do Circuito 9a, é atribuído diretamente ao bit de maior ordem do resto (R7) e aos valores Sop e Cin do circuito, determinando assim se há ou não lugar a inversão de sinal.
No Passo 15 do algoritmo diz-se: “Atribui-se ao resultado o sinal calculado no passo 2”.
Também aqui vamos ter que reconverter os resultado da operação, que foi feita com números positivos, de acordo com o sinal determinado para ele. Para isso vamos usar um Circuito Inversor de Sinal a que vamos chamar Circuito 7. Neste caso, o sinal é aquele que foi calculado no passo 2 e cujo valor é fornecido pelo Circuito 9a. O seu valor é atribuído diretamente ao bit de maior ordem do resultado (Q7) e aos valores Sop e Cin do circuito, determinando assim se há ou não lugar a inversão de sinal. O valor do resultado é o valor do quociente e portanto o que está presente no Registo 5.
