Pixel e RGB

Introdução

O computador começa a fazer parte do dia-a-dia comum dos cidadãos. Passamos rapidamente da alfabetização à computorização. Em breve, quem não for computorizado, será analfabeto.

Tudo está a ser digitalizado no mundo em que hoje vivemos.

As Imagens são praticamente todas em formato digital, e quem as tem ainda em formato analógico, procura a sua conversão. Os fotógrafos profissionais já utilizam a fotografia digital, que atingiu níveis de fiabilidade espantosos. Quem não tem hoje uma máquina digital, nem que seja no telemóvel?

As músicas já estão todas em formato digital. Desde o aparecimento do CD que assim tem acontecido. Já são mesmo gravadas diretamente em formato digital. A maioria dos gravadores de som já usa o formato digital. Podemos portanto dizer que também o som já está quase, exclusivamente, em formato digital.

A Televisão acabou agora com as transmissões analógicas e introduziu a TDT (Televisão Digital Terrestre). Os filmes estão todos à disposição do vulgar cidadão, em formato digital, com as melhores qualidades de imagem e som.

O fabuloso mundo da Internet tem vindo a evoluir para níveis espantosos de interligação das pessoas. Já quase tudo se pode fazer pela Internet. Compras, vendas, consultas, leituras, estudos, investigação, questões burocráticas pessoais, questões fiscais, etc.

Digamos antes, que já pouco se pode fazer sem a Internet.

O correio entre as pessoas está lentamente a evoluir para o correio eletrónico. Os arquivos físicos começam a ser, em parte, substituídos por arquivos em formato digital, e a evolução será sempre no sentido de este formato vir a substituir o físico. Até por questões ecológicas.

Com a descida do valor do armazenamento em disco e o aumento rápido da capacidade dos mesmos, mais se acentuará a “numeralização” do nosso mundo.

Numeralização, foi o que dissemos. Porquê?

Porque, como já sabem, a representação digital é uma representação em números, no sistema binário.

Mas a imagem que o computador nos transmite, aquilo que aparece no monitor, gráficos e texto, não têm nada de numérico. São bem reais e com aspeto normal para um humano. Como é que podem ser constituídas por números, e ter aquele aspeto?

Então vamos lá ver como é que o computador, só com zeros e uns, consegue mostrar-nos os gráficos com que trabalhamos, e através dos quais comunica connosco. Como consegue converter em números e mostrar-nos num ecrã as nossas fotografias, e como consegue converter em números e fazer-nos ouvir as músicas de que mais gostamos.

Como aparece a imagem no Monitor

Uma fotografia, um texto, uma janela de um programa, tudo são gráficos para o computador. A letra A, por exemplo, que tem para nós um significado específico, é para o computador nada mais, nada menos, que outro gráfico. Ele só entende os números binários que são necessários para compor os gráficos no monitor.

E como é que o computador escreve no monitor ou desenha no monitor?

Vamos começar por analisar uma imagem num monitor LCD, na Figura 1.

Perfeita, bem definida e contrastada.

Agora vamos aproximar-nos do monitor o suficiente para conseguir ver a imagem aumentada 6 vezes.

Para fazermos isto temos de usar uma lente que provoque esse aumento. Ficará como na Figura 2.

A definição baixou e as linhas parecem quebradas em Ziguezague.

Significa isto que se começa a notar a estrutura que constrói uma imagem no ecrã, a qual, devido à aproximação, ultrapassou os limites próprios de definição.

Com a tal lente conseguem-se ver uma multiplicidade de pequenos quadradinhos coloridos.

Vamos agora ver na Figura 3 o ecrã do monitor com uma lente que o amplie 34 vezes.

Já se percebe a razão da menor definição das linhas. Os pequeninos quadrados da imagem anterior

aumentaram substancialmente e agora as linhas parecem escadas construídas com muitos quadrados com várias tonalidades da cor das linhas e das cores circundantes

Parece que afinal, a imagem é construída por muitos quadrados, coloridos de forma a darem à imagem o aspeto com que a nossa visão a vê sem a ampliação, em que não consegue distinguir os quadrados individualmente.

E é efetivamente isso que acontece. E os ditos quadrados dão pelo nome de Pixels (Picture elements).

O ecrã de um monitor LCD é constituído por muitos destes quadrados. Vamos analisar, em concreto, um monitor Full HD e aspeto 16:9, com uma resolução de 1920 colunas por 1080 linhas, ou seja, com 1920 x 1080 pixels, os quadradinhos que vimos atrás, num total de 2.073.680 pixels. Admitindo que o nosso monitor tem uma área de 1545 cm², cada pixel terá a área de 0,075 mm², ou melhor dizendo, o quadrado formado pelo pixel terá 0,27 mm de lado.

Resumindo, cada imagem apresentada no ecrã do nosso monitor é definida por 2.073.680 pixels.

Mas como?

Cada pixel pode assumir uma e uma só cor, desde o branco até ao preto, passando por todo o espetro solar. E tantas mais são as cores, quando maior for a profundidade de bits.

E o que é isso da profundidade de bits?

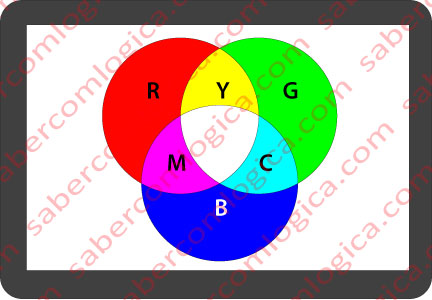
Comecemos então por fazer referência às letras R, G e B, que pronunciaremos como RGB. Significam Red, Green e Blue (Vermelho, Verde e Azul). Com estas 3 cores, conseguem-se construir todas as outras. Os monitores LCD, como aquele de que estamos a falar, funcionam com o processo de cor RGB.

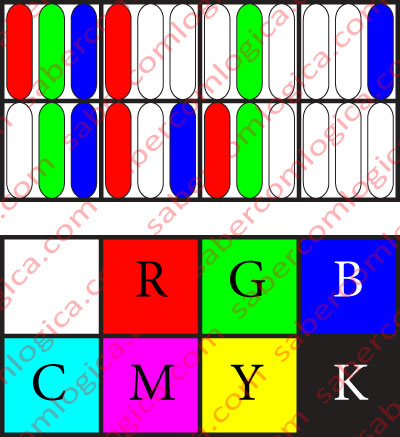
Vejamos na Figura 4 como cada pixel é constituído por três micro lâmpadas (vamos chamar assim aos emissores de luz), com filtros que só permitem que cada uma produza Red, Green ou Blue, com a saturação que lhe for definida. A saturação é a quantidade de uma dada cor ou a intensidade de luz da lâmpada que produz essa cor, definida de 0 a 100%.

Significa então que temos de controlar isoladamente 3 x 2.073.680 = 6.221.040 micro lâmpadas em cada imagem que se coloca no ecrã.

A referência a micro lâmpadas é usada exclusivamente para facilidade de compreensão do processo. Um monitor LCD tem o seu funcionamento baseado na forma e disposição que dá a cristais em meio líquido (Liquid Crystal Display) retro iluminados, mas não está no âmbito deste trabalho analisá-los. Os ecrãs LED funcionam como estes, com a diferença de a retroiluminação ser feita por lâmpadas LED, mais intensas, mais regulares e mais económicas. Só agora está em expansão, ainda em fase experimental, um verdadeiro ecrã a que o nome LED se apropria, pois cada pixel é efetivamente composto por 3 micro lâmpadas LED.

Adiante. Por simplicidade, vamos então imaginar cada pixel com 3 lâmpadas.

O processo de definição da intensidade de cada cor pode ter várias profundidades de bits. Cada cor usa um determinado número de bits para definir a variação de intensidade da sua lâmpada (regulando o potenciómetro). A união dos bits das 3 cores constitui aquilo a que chamamos Profundidade de Bits.

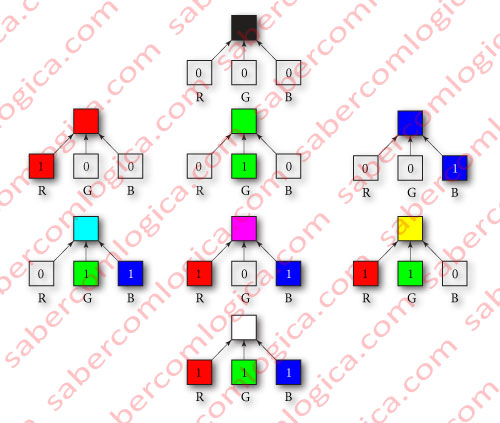
Na Figura 5 podemos ver um quadro onde a profundidade de bit foi definida a 3, isto é, 1 bit para cada cor. Cada uma das cores só pode ter dois estados: “Ou tudo, ou nada”, isto é:

• 0, com 0% saturação, ou com a respetiva lâmpada desligada.
• 1, com 100% de saturação ou com a lâmpada ligada com toda a intensidade.

Isto quer dizer que temos a lâmpada ligada a um interruptor e não a um potenciómetro. Pode estar ligada ou desligada. Nessa figura, o quadrado acima dos 3 quadrados RGB representa a cor que se obtém da combinação dos referidos 3, de acordo com a intensidade definida para cada um.

Na Figura 4 representa-se o mesmo conceito, de uma forma diferente. Nos 8 quadrados de cima, mostra-se o estado das lâmpadas que compõem o pixel, e nos 8 quadrados de baixo a cor que é obtida para esse mesmo pixel correspondente ao estado dessas lâmpadas.

O processo de cor RGB é um processo aditivo. O quadro que vimos mostra claramente que as diversas cores se vão obtendo juntando valores de saturação (1) das outras cores, ao preto (0,0,0). Assim, das diversas possíveis combinações resulta:

• Desligando todas (0,0,0), o Preto (K).
• Ligando só a Vermelha (1,0,0), o Red (R)
• Ligando só a Verde (0,1,0), o Green (G)
• Ligando só a Azul (0,0,1), o Blue (B)
• Ligando Verde e Azul (0,1,1), o Cyan (C).
• Ligando Vermelha e Azul (1,0,1), o Magenta (M).
• Ligando Verde e Vermelha (1,0,0), o Yellow (Y).
• Ligando todas (1,1,1), o Branco.

Podemos perceber esta evidência através de um caso prático. Imaginemos que estamos dentro de um quarto todo branco e com 3 lâmpadas (R, G e B). Se estiverem todas apagadas, o quarto está às escuras, portanto terá as paredes pretas. Por cada cor que ligamos, as paredes ficam com a cor dessa lâmpada. Se ligarmos todas, o quarto fica totalmente iluminado, com as paredes brancas. É isto que se entende por processo aditivo.

Escrevemos propositadamente o nome das cores em Inglês para fazer sobressair a primeira letra do nome de cada cor. Reparem que as 3 cores, geradas pela adição de 1 de cada duas das outras, dá origem a outro processo de cor, o CMYK (o K refere-se ao preto). É este o processo de cores usado para comunicar com as impressoras. Certamente já repararam que as impressoras a cores utilizam 4 tinteiros com as cores C, M, Y e K, ou 2 tinteiros, sendo um com preto (K) e outro com as outras 3 cores (C, M, e Y).

É evidente que as imagens seriam muito monótonas com um sistema de 8 cores (2³). Há já muito tempo atrás (em termos informáticos), eram usadas 16 e 256 cores. As placas gráficas mais modernas já só suportam, no mínimo, as 65.536 cores, que correspondem a uma profundidade de 16 bits. Neste último caso, como 16 não é divisível por 3, foram atribuídos 5 bits ao vermelho, 5 ao azul e 6 ao verde.

A profundidade de bits que é hoje utilizada em praticamente todos os monitores a cores é de 24 bits ou True Color. Assim, teremos 8 bits para cada cor RGB, isto é, o valor de saturação de cada cor pode ir de 0 a 255, num total de 256 valores por cor. A esta combinação de 256 x 256 x 256 correspondem cerca de 16,7 milhões de cores, resultantes dos diferentes valores de saturação de cada uma das cores RGB.

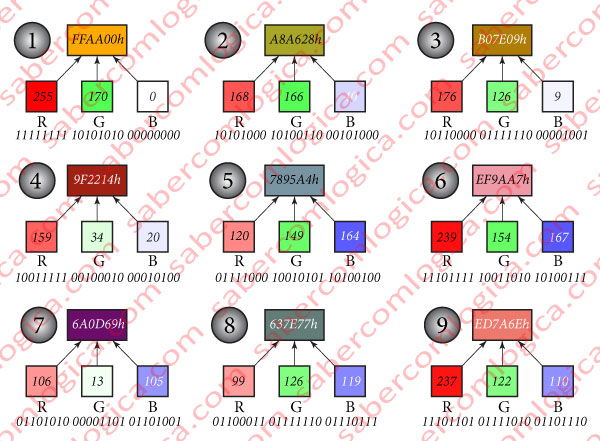
Na Figura 6 apresentamos 9 dessas possíveis combinações, representadas em retângulos. Por baixo de cada uma dessas cores temos 3 quadrados, cada um representando o valor da saturação de cada uma das cores R, G e B que contribui para a cor final. O valor decimal de saturação dessa cor (0 a 255) está inscrito dentro do quadrado. Por baixo do quadrado é apresentado o valor binário correspondente a essa cor e dentro do retângulo da cor resultante é inscrita a sua notação hexadecimal, que é de uso muito frequente em desenho gráfico.

Por exemplo, para a cor 8, a sua representação para a máquina será

01100011 01111110 01110111

para um humano será

637E77h

em que o h indica a representação em hexadecimal, ou

99R – 126G – 119B

em decimal, pelo valor de saturação de cada cor (de 0 a 255).

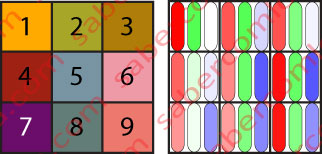
Na Figura 7 pode-se verificar a correspondência entre a cor resultante para o Pixel (à esquerda na imagem) e a saturação de cada uma das micro lâmpadas do referido pixel (à direita na imagem), para as mesmas cores da Figura 6.

É natural que nalguns casos não se consigam distinguir as diferenças de saturação na mesma cor, pois:

• Em caso de impressão em papel, os limites de saturação CMYK, para efeitos de impressão, (dependentes do perfil da impressora) são diferentes dos RGB até agora vistos, isto é, não se conseguem atingir os 0% nem os 100%, o que é por vezes compensado com a utilização dos pretos (K), mas ficando sempre longe dos extremos.
• Mesmo em RGB e num ecrã, a representação de uma cor em valores muito próximos não é para nós sensível. No entanto, quando representada numa fotografia de alta definição, embora pontualmente não se perceba a diferença, globalmente é precisamente essa diferença que torna a fotografia mais definida e contrastada.

Um pouco atrás relacionámos 24 bits com True Color. Mas o que está escrito em muitos sítios é que a True Color corresponde a uma profundidade de 32 bits. Em que ficamos?

É verdade. Efetivamente, por uma questão de alinhamento com leituras de memória em submúltiplos de 64 bits (a largura de banda de um DIMM), concluiu-se que era mais rápido fazer a leitura em memória a múltiplos de cadeias de 32 bits, também o tamanho da palavra dos processadores de 32 bits.

Então, em nome da eficiência, juntaram-se mais 8 bits aos 24, passando a ter 32 bits por pixel, embora se mantenha exatamente a mesma informação relativamente às cores R, G e B, isto é, 8 bits por cor, cerca de 16,7 milhões de cores no total.

Atualmente, as placas gráficas utilizam estes 8 bits adicionais para juntar à definição da imagem a sua transparência, que poderá assim ter valores entre 0 e 255, ou seja de opaca, a totalmente transparente. A transparência é hoje em dia um fator importante em qualquer imagem.

Portanto, para cada pixel temos 32 bits de informação, representando cerca de 16,7 milhões de cores possíveis com 256 diferentes graus de transparência.

Então, por cada imagem a colocar no ecrã, teremos de enviar para o monitor 2.073.680 x 32= 66.357.760 bits. A uma taxa de refrescamento de 50 Hz (número de vezes por segundo que a imagem no ecrã é renovada) teremos um fluxo de 66.357.760 x 50 = 3.317.888.000 bits/s ou seja, cerca de 400 MB/s.

No artigo seguinte vamos analisar os tipos de imagem digital.