Portas Lógicas

As portas lógicas são a transposição através de circuitos elétricos reais do computador, conseguidos pela junção de transístores, do comportamento dos operadores lógicos da nossa abstração matemática.

Observação: As resistências que estão inseridas nos circuitos têm a única função de impedir curto-circuitos que queimariam o transístor quando este não oferecesse qualquer resistência ao fluxo de corrente elétrica.

Porta NOT

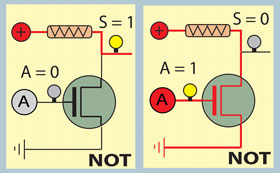
Analisando o comportamento do circuito , verificamos que dispõe de uma linha de ligação entre a alimentação e a terra, na qual está interposto um transístor. Portanto, a passagem de corrente entre a alimentação e a terra só é condicionada pelo estado do transístor.
Se a Porta do transístor estiver sujeita a tensão (estado lógico 1 ou lâmpada acesa), o transístor terá uma impedância praticamente nula, isto é, estará no estado condutor, fornecendo assim o caminho preferencial para o fluxo de corrente elétrica, que segue sempre o caminho com menor resistência (a lâmpada S funciona como  uma resistência). Como consequência a lâmpada S mantém-se apagada, isto é, a saída do circuito não tem tensão (S=0).
Se a Porta do transístor não estiver sujeita a tensão (estado lógico 0 ou lâmpada apagada), o mesmo terá uma impedância infinita, isto é, estará no estado isolante. Nestas circunstâncias a corrente elétrica flui pelo circuito onde está inserida a lâmpada S, que acende, significando isso que a saída do circuito está em tensão (S=1).

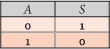
Podemos assim construir a tabela verdade deste circuito. Se preenchermos os valores da tabela pelo estado da lâmpada, isto é, acesa ou apagada, substituindo posteriormente essas palavras pelos seus significados(estados lógicos 1 ou 0), verificamos que a tabela resultante corresponde à do operador lógico NOT.
Assim já podemos concluir que a ação que imaginámos em abstrato para o operador NOT pode ser materializada através de um circuito elétrico que reproduz o comportamento do mesmo.
A expressão algébrica booleana para o circuito será:

NOT A ou ¬A

Porta NAND

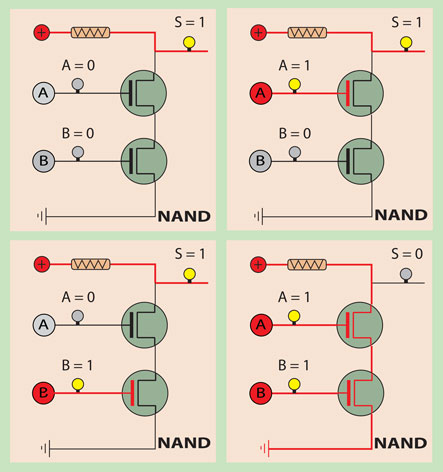
Na linha de passagem entre a alimentação e a terra estão interpostos dois transístores colocados em série. Assim, a corrente elétrica só flui entre a alimentação e a terra se ambos os transístores estiverem no estado condutor.
Para que isso aconteça é necessário que as Portas dos dois estejam com tensão (estado lógico 1 ou lâmpada acesa). E é só nesta situação que o circuito fica sem tensão (estado lógico 0 ou lâmpada apagada) na sua saída S, pois a corrente elétrica flui pelo lado com menor resistência, ou seja, pela linha onde se encontram os transístores que não oferecem resistência.

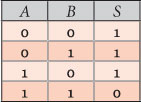
Construída a tabela verdade deste circuito e comparada com as tabelas verdade dos operadores lógicos concluímos que este circuito representa o comportamento do operador lógico NAND.
Desta forma, também a ação que imaginámos em abstrato para o operador NAND pode ser materializada através de um circuito elétrico que reproduz o comportamento do mesmo.
A expressão algébrica booleana  para o circuito, reduzida aos operadores básicos, será:

A NAND B = NOT(A AND B) ou ¬(A•B)

Porta NOR

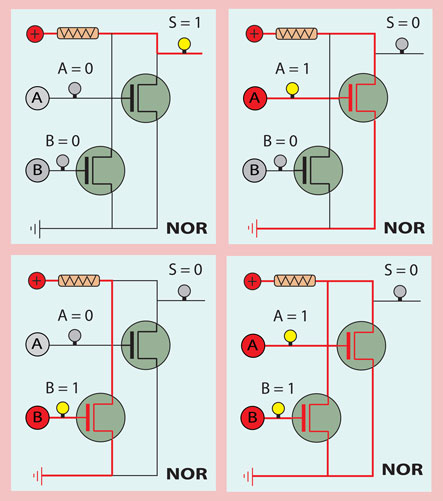
A solução para esta porta consiste em  dois transístores colocados em dois circuitos paralelos entre a fonte de tensão e a terra, que criam dois caminhos paralelos para a corrente elétrica poder fluir.
Desde que algum dos transístores interposto no caminho esteja no estado condutor, isto é, desde que a sua porta esteja submetida a tensão (estado lógico 1), então a corrente flui diretamente de mais para menos e a saída S permanece a 0.
Só no caso de nenhum dos dois transístores ter tensão na porta, estando portanto no estado isolante (estado lógico 0), a corrente elétrica não flui através dos transístores e sai pela saída S acendendo a respetiva lâmpada.

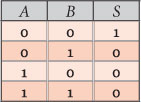
Construída a tabela verdade deste circuito, conforme a Figura 6 e comparada com as tabelas verdade dos operadores lógicos, verifica-se a sua equivalência à tabela do operador NOR.
Assim, também já podemos concluir que a ação que imaginámos em abstrato para o operador NOR pode ser materializada através de um circuito elétrico que reproduz o comportamento do mesmo.
A expressão algébrica booleana para o circuito será:

A NOR B = NOT (A OR B) ou ¬(A+B)

Introdução às restantes portas

E se agora, assim de repente, vos disséssemos que com os três circuitos elementares NOT, NAND e NOR (um transístor, dois transístores em série e dois transístores em paralelo) já temos tudo o que precisamos saber em termos de conversão em circuitos elétricos para podermos materializar todos os circuitos do computador?

Só podem estar a gozar connosco! Um computador? Essa máquina altamente sofisticada? Da qual cada vez mais somos dependentes para as nossa atividades diárias? Que gere quase todos os automatismos por que passamos durante o dia? Não, não pode ser verdade!
Mas é verdade. Na realidade, essa máquina que efetivamente é altamente complexa, que integra circuitos de uma enorme complexidade, decompõe-se numa base da mais elementar simplicidade. Agora só precisamos de combinar a base de extrema simplicidade em sucessivas interligações que poderão levar aos mais sofisticados circuitos de cálculo que integram os processadores de última geração.
E, para o entender basta que evoluamos lentamente. Podemos é levar muito tempo a chegar lá. Mas se tivermos sempre o cuidado de entender o raciocínio lógico  de cada passo, isto é, não só o que faz mas porque é que o faz, chegamos lá.

Vamos agora começar a abordar uma outra etapa do conhecimento dos circuitos elétricos que nos permitirá continuar a evoluir no seu conhecimento. Consiste essa etapa no facto de as saídas de um circuito poderem ser as entradas de outros, obtendo assim operações lógicas sequenciais com estes circuitos elementares.

Em termos de análise lógica abstrata, tratámos primeiro o operador AND e só depois o operador NAND, como um seu derivado, a sua negação. Da mesma forma tratamos primeiro o operador OR e depois o operador NOR, como um seu derivado, também a sua negação.
Efetivamente na lógica booleana há três operadores fundamentais: NOT, AND e OR. Destes derivaram todos os outros. E em termos de análise lógica continua a ser verdade.

Mas em termos de construção de circuitos elétricos verificamos que temos de o fazer de forma diferente, pela simplicidade dos circuitos que representam o NAND e o NOR, partindo destes para obter os seguintes.
Por essa razão vamos continuar a apresentar a expressão algébrica booleana para cada circuito. Se interpretarem literalmente a tradução da linguagem do circuito elétrico, verão que corresponde ao significado do operador lógico que materializa.
Em álgebra booleana, tal como na álgebra numérica, a precedência das operações é a mesma, isto é, resolvem-se primeiro as operações entre parênteses, respeitando a sua ordenação.
Vejam sempre o operador NOT como um inversor. Liga o desligado e desliga o ligado. Torna verdadeiro o falso e falso o verdadeiro. Torna 0 em 1 e 1 em 0.

Porta AND

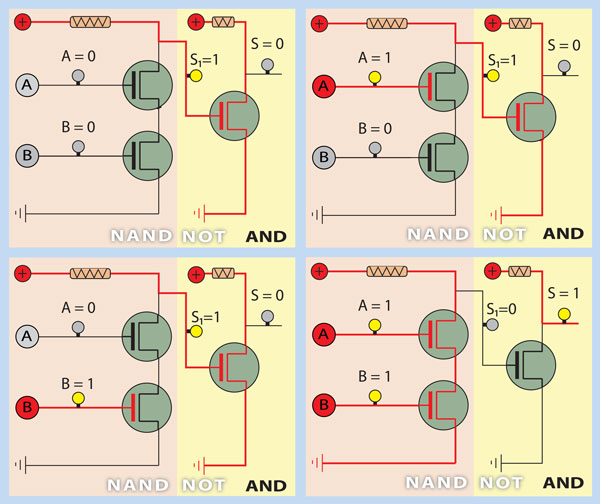
Analisando a Figura 7, onde continuamos a contemplar as 4 possíveis combinações de estado das entradas A e B, verificamos que o mesmo corresponde à ligação da saída de uma porta NAND à entrada de uma porta NOT, ou seja, à inversão do valor da saída da porta NAND. A negação da negação corresponde à afirmação, isto é, NOT NAND corresponde a AND.

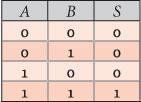
Se construirmos a sua tabela verdade analisando o comportamento dos transístores para as diversas combinações de alimentação das suas portas e a compararmos com as tabelas dos operadores lógicos concluímos que esse circuito materializa o operador AND.

Será a seguinte a expressão algébrica booleana para o circuito:

A AND B  ou  A•B
NOT (A NAND B) = NOT (NOT (A AND B))   ou   ¬(¬(A•B))  

Porta OR

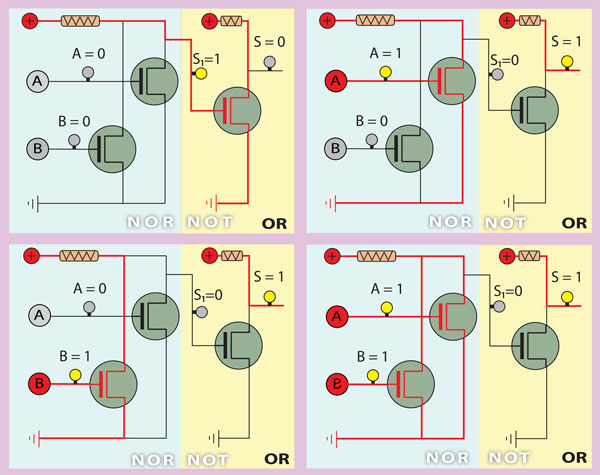
Analisando a Figura 9, que continua a contemplar as 4 possíveis combinações de estado das entradas A e B,verificamos que o mesmo corresponde à ligação da saída de uma porta NOR à entrada de uma porta NOT, ou seja, à inversão do valor da saída da porta NOR. Mais uma vez, a negação da negação corresponde à afirmação, isto é, NOT NOR corresponde a OR.

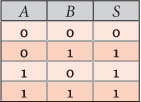
Se construirmos a sua tabela verdade, analisando o comportamento dos transístores para as diversas combinações de alimentação das suas portas e a compararmos com as tabelas dos operadores lógicos concluímos que esse circuito materializa o operador OR.

Será a seguinte a expressão algébrica booleana para o circuito:

A OR B  ou  A+B
 NOT (A NOR B) = NOT (NOT (A OR B))  ou  ¬(¬(A+B))

Porta XOR

Vamos usar raciocínio lógico para, com a  combinação das portas que já conhecemos obtermos o comportamento pretendido. O que queremos obter? O que precisamos ter na saída do circuito por cada combinação das entradas A e B?

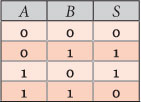
Comecemos por analisar a tabela verdade do operador XOR. Como podemos constatar, o resultado só é verdade quando as entradas A e B são diferentes.
Nenhuma das portas já analisadas tem esse comportamento, para as combinações possíveis de A e B.

Para podermos utilizar as portas que já conhecemos para resolver este problema, as combinações de A e B nas suas entradas têm que ser diferentes.
Então vamos ter que trabalhar previamente A e B em outras portas para que as suas saídas, colocadas como entradas numa qualquer outra porta simulem o comportamento do operador XOR.

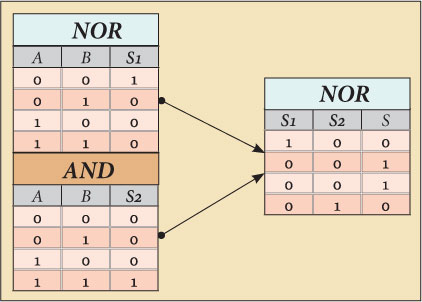
Vamos experimentar com uma porta NOR à saída do circuito. Como se sabe NOR devolve verdadeiro (1) exclusivamente quando as duas entradas são falsas (0).
Vamos chamar S1 e S2 às entradas da porta NOR. Então S1 e S2 vão ter que ser ambas 0 quando A e B forem diferentes e ambas 1 quando A e B forem iguais.
Ou por outras palavras S1 e S2 devem assumir a combinação 10,00,00,01 correspondentes respetivamente às combinações 00,01,10,11 de A e B.

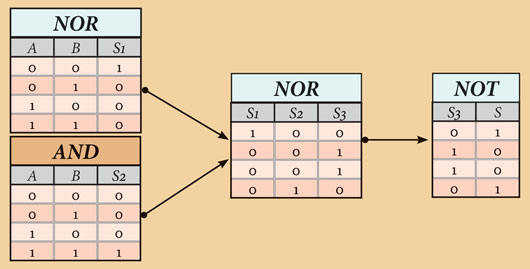
Então vejamos acompanhando a evolução das tabelas verdade compostas dos diferentes operadores  até chegarmos à tabela verdade do operador XOR. Não esquecer que a tabela verdade que se pretende é para as entradas A e B e para a saída S.:

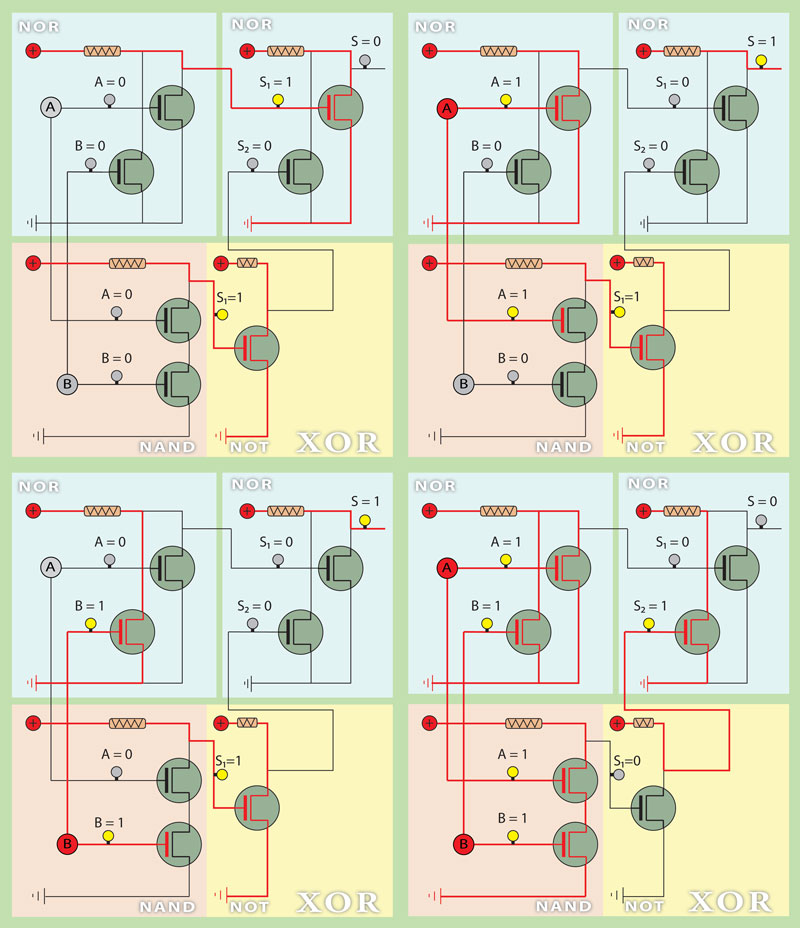
Uma porta NOR devolve na sua saída os valores de S1 para as combinações de A e B  [AB→S1=(00→1, 01→0, 10→0 and 11→0)].

Uma porta AND devolve na sua saída os valores de S2 para as combinações de A e B  [AB→S2=(00→0, 01→0, 10→0 and 11→1)].
Agora só temos que ligar A e B às entradas de duas portas AND e NOR e as saídas destas às entradas de uma outra porta NOR, que por sua vez devolverá os valores que pretendemos para as combinações possíveis de A e B.

Temos a solução. Vamos verificar no próprio circuito, voltando a construir a tabela verdade acompanhando o comportamento dos transístores pela evolução dos valores nas suas portas.

O circuito apresentado  retrata o circuito elétrico correspondente à combinação de operadores pretendida, decomposta nas portas essenciais NOT, NAND e NOR.

A expressão algébrica booleana para o circuito elétrico XOR reduzida aos operadores booleanos básicos é:

A XOR B  ou  A⊕B = (A NOR B) NOR (A AND B) = NOT (NOT (A OR B) OR (A AND B))  ou  ¬(¬(A+B)+(A•B))

Para conseguirmos um circuito com o comportamento que pretendíamos definimos passo a passo as operações a executar para obtermos o fim desejado, isto é, decompusemos a operação total nas suas mais pequenas componentes, ou antes, definimos o ALGORITMO do problema.

Algoritmo? O que é lá isso?

Algoritmo

Um algoritmo é a representação dos passos necessários para realizar uma operação, de uma forma tão mais decomposta quanto possível.
Por exemplo, uma receita de culinária é um algoritmo.

Tecnicamente, um algoritmo é uma sequência finita de instruções bem definidas e não ambíguas, cada uma das quais pode ser executada mecanicamente num período de tempo finito e com uma quantidade de esforço finita.

Um algoritmo, não representa necessariamente um programa de computador, mas sim os passos necessários para realizar uma tarefa. E a sua implementação pode ser feita por um computador, por outro tipo de autómato ou mesmo por um ser humano.
Um algoritmo corretamente executado não irá resolver um problema se estiver incorretamente implementado  ou se não for apropriado ao problema.
Por exemplo, um algoritmo que descreva a forma como nos vestimos pode especificar:
“primeiro vista as meias, depois calce os sapatos, depois vista as calças e finalmente vista a camisa”
enquanto outro algoritmo para o mesmo fim pode especificar:
“primeiro vista a camisa, depois as calças, depois vista as meias e finalmente calce os sapatos”.
Fica claro que o primeiro algoritmo conduz a um resultado muito menos eficaz e correto do que o segundo, apesar de ambos levarem ao mesmo resultado.
Porquê tanta conversa sobre um algoritmo?
Porque vai ser muito utilizado ao longo deste trabalho.  Porque qualquer raciocínio lógico deve começar pela criação de um algoritmo que defina os passos mais elementares (não decomponíveis) desse mesmo raciocínio.
Os algoritmos não têm que ser obrigatoriamente escritos. Mas devem fazer sempre parte do processo de organização mental que conduz a deduções, na sequência de um qualquer raciocínio lógico.
Como facilmente se depreende, um programa de computador é essencialmente um algoritmo que diz ao computador os passos específicos para executar uma tarefa e em que ordem devem ser executados. E como o computador é uma máquina de essência básica e simples esse algoritmo tem que ser destrinçado ao mais ínfimo passo.
Para qualquer processo computacional, o algoritmo precisa estar rigorosamente definido, especificando a maneira como se comportará em todas as circunstâncias.

Porta XNOR

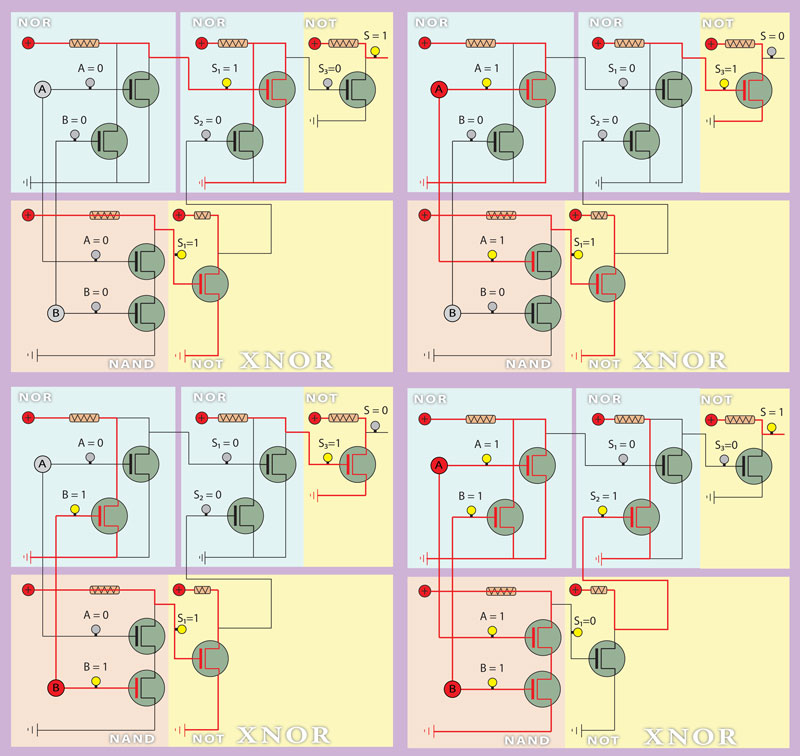
Este circuito pode ser obtido por processo idêntico ao anterior, na sequência de um raciocínio lógico que leve à determinação do algoritmo do problema, o que nos levaria a uma solução diferente  da apresentada. Porque não se pretende complicar mais o trabalho optámos pela simples negação do operador XOR, por introdução de uma porta NOT na sua saída, o que se encontra refletido na figura acima onde apresentamos o circuito.

A verdade encontra-se precisamente onde ambas as proposições são  verdadeiras ou falsas, isto é, coincidentes. Daí o nome de operador coincidência. Ora isto consegue-se pela aplicação à saída do circuito anterior de um circuito inversor, ou seja, um NOT.

Aqui junto na Figura 15, temos a Tabela verdade composta pelas tabelas verdade dos  operadores que materializam este circuito tal como o apresentamos.

 

Verifica-se pela tabela verdade global e final obtida pela análise do comportamento dos transístores do circuito para as diferentes combinações das entradas A e B, que o comportamento deste circuito é igual à do operador XNOR, pelo que se pode concluir que este circuito materializa o comportamento desse operador.

Deixamos a cada um a tentativa de elaboração de um raciocínio lógico para a  obtenção de uma solução diferente e própria para a construção do circuito que materializa este operador. Que tal experimentarem substituir a porta final de saída do circuito por uma porta NAND?

Vamos então ver a expressão algébrica booleana para o circuito do operador XNOR.

A XNOR B  ou  A≡B  ou  ¬(A⊕B)
NOT ((A NOR B) NOR (A AND B)) = NOT (NOT (NOT (A OR B) OR (A AND B)))  ou  ¬(¬(¬(A+B)+(A•B)))

Porta Tristate

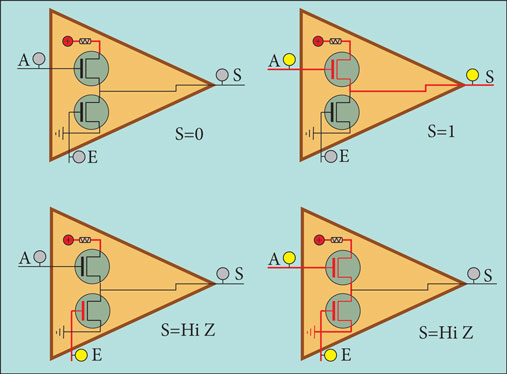
Vamos representar os circuitos elétricos para estas portas para a situação de ativa a 0, como na Figura. Assim, a porta está ativa quando E está a 0, caso em que a informação passa de A para S, seja 0 ou 1. Quando E está a 1, não passa nada.
Reparem como E, ao ativar o transístor a que está ligado, absorve o valor gerado pelo transístor ligado à entrada A, funcionando assim como um interruptor, respeitando a Tabela verdade desta Porta Lógica.

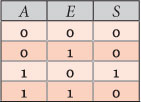
Juntamos a tabela verdade para esta porta, conseguida pela análise do comportamento dos transístores de acorco com as diferentes combinações das entradas A e E, em que E representa a situação de Enable que para este caso é ativo a 0.